《2025年1课3练江苏人民出版社九年级数学下册北师大版》

5. (2024·深圳宝安区二模)如图(1)，在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$D$为$AC$上一点，$CD=\sqrt{2}$，动点$P$以每秒$1$个单位长度的速度从点$C$出发，在三角形边上沿$C\rightarrow B\rightarrow A$匀速运动，到达点$A$时停止，以$DP$为边作正方形$DPEF$. 设点$P$的运动时间为$t$秒，正方形$DPEF$的面积为$S$，当点$P$由点$B$运动到点$A$时，经探究发现$S$是关于$t$的二次函数，并绘制成如图(2)所示的图象. 由图象可知线段$AB$的长为(　　　)．
　　　
A. 7
B. 6
C. 5
D. 4

答案： B [解析]在$Rt\triangle PCD$中，$CD=\sqrt{2}$，$PC = t$，则$S = PD^{2}=t^{2}+(\sqrt{2})^{2}=t^{2}+2$，
当$S = 6$时，$6=t^{2}+2$，解得$t = 2$（负值已舍去），
∴$BC = 2$，
∴抛物线经过点$(2,6)$。
由抛物线顶点为$(4,2)$，
可设抛物线表达式为$S = a(t - 4)^{2}+2$，
将$(2,6)$代入，得$6 = a(2 - 4)^{2}+2$，解得$a = 1$，
∴$S=(t - 4)^{2}+2$，
当$y = 18$时，$18=(t - 4)^{2}+2$，$t = 0$（舍去）或$t = 8$，
∴$AB=(8 - 2)\times1 = 6$。故选B。

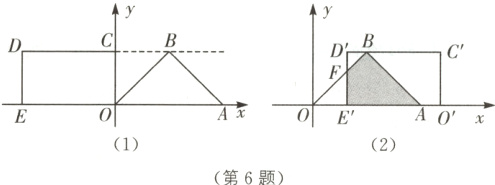
6. 中考新考法 探究动图问题 在平面直角坐标系中，$O$为原点，$\triangle OAB$是等腰直角三角形，$\angle OBA = 90^{\circ}$，$BO = BA$，顶点$A(4,0)$，点$B$在第一象限，矩形$OCDE$的顶点$E(-\frac{7}{2},0)$，点$C$在$y$轴的正半轴上，点$D$在第二象限，射线$DC$经过点$B$.
(1)如图(1)，求点$B$的坐标.
(2)将矩形$OCDE$沿$x$轴向右平移，得到矩形$O'C'D'E'$，点$O$，$C$，$D$，$E$的对应点分别为$O'$，$C'$，$D'$，$E'$. 设$OO' = t$，矩形$O'C'D'E'$与$\triangle OAB$重叠部分的面积为$S$.
①如图(2)，当点$E'$在$x$轴正半轴上，且矩形$O'C'D'E'$与$\triangle OAB$重叠部分为四边形时，$D'E'$与$OB$相交于点$F$，试用含有$t$的式子表示$S$，并直接写出$t$的取值范围；
②当$\frac{5}{2}\leqslant t\leqslant\frac{9}{2}$时，求$S$的取值范围(直接写出结果即可).

答案：

(1)如图
(1)，过点$B$作$BH\perp OA$，垂足为$H$。

由点$A(4,0)$，得$OA = 4$。
∵$BO = BA$，$BH\perp OA$，
∴$OH=\frac{1}{2}OA = 2$。
又$\angle OBA = 90^{\circ}$，$\angle BOH = 45^{\circ}$，
∴$\triangle OBH$为等腰直角三角形，
∴$BH = OH = 2$，
∴点$B$的坐标为$(2,2)$。
(2)①由点$E(-\frac{7}{2},0)$，得$OE=\frac{7}{2}$。
由平移知，四边形$O'C'D'E'$是矩形，
∴$\angle O'E'D' = 90^{\circ}$，$O'E' = OE=\frac{7}{2}$。
∴$OE'=OO'-O'E'=t-\frac{7}{2}$，$\angle FE'O = 90^{\circ}$。
∵$BO = BA$，$\angle OBA = 90^{\circ}$，
∴$\angle BOA=\angle BAO = 45^{\circ}$，
∴$\angle OFE' = 90^{\circ}-\angle BOA = 45^{\circ}$，
∴$\angle FOE'=\angle OFE'$，
∴$FE' = OE'=t-\frac{7}{2}$，
∴$S_{\triangle FOE'}=\frac{1}{2}OE'\cdot FE'=\frac{1}{2}(t-\frac{7}{2})^{2}$，
∴$S = S_{\triangle OAB}-S_{\triangle FOE'}=\frac{1}{2}\times4\times2-\frac{1}{2}(t-\frac{7}{2})^{2}$，
整理，得$S=-\frac{1}{2}t^{2}+\frac{7}{2}t-\frac{17}{8}$。
当点$O'$与点$A$重合时，矩形$O'C'D'E'$与$\triangle OAB$重叠部分刚开始为四边形，如图
(2)，此时$OO'=t = 4$；

当点$D'$与点$B$重合时，矩形$O'C'D'E'$与$\triangle OAB$重叠部分为三角形，接下来往右平移时重叠部分一直为三角形直到点$E'$与点$A$重合，如图
(3)。

此时$t = OO'=EE'=\frac{7}{2}+2=\frac{11}{2}$，
∴$t$的取值范围是$4\leqslant t＜\frac{11}{2}$。
故$S=-\frac{1}{2}t^{2}+\frac{7}{2}t-\frac{17}{8}$，其中$4\leqslant t＜\frac{11}{2}$。
②分段讨论：(ⅰ)当$\frac{5}{2}\leqslant t\leqslant\frac{7}{2}$时，矩形$O'C'D'E'$与$\triangle OAB$的重叠部分如图
(4)所示。

此时$AO' = 4 - t$，$\angle BAO = 45^{\circ}$，$\triangle AO'F$为等腰直角三角形，
∴$AO' = FO' = 4 - t$，
∴$S_{\triangle AO'F}=\frac{1}{2}AO'\cdot FO'=\frac{1}{2}(4 - t)^{2}$，
∴重叠部分面积$S = S_{\triangle AOB}-S_{\triangle AO'F}=4-\frac{1}{2}(4 - t)^{2}=-\frac{1}{2}(t - 4)^{2}+4$，
∴$S$是关于$t$的二次函数，且对称轴为直线$t = 4$，开口向下，
∴自变量离对称轴越远，其对应的函数值越小，
∴将$t=\frac{7}{2}$代入，得最大值$S=-\frac{1}{2}\times(\frac{7}{2}-4)^{2}+4=\frac{31}{8}$，将$t=\frac{5}{2}$代入，得最小值$S=-\frac{1}{2}\times(\frac{5}{2}-4)^{2}+4=\frac{23}{8}$。
∴当$\frac{5}{2}\leqslant t\leqslant\frac{7}{2}$时，$\frac{23}{8}\leqslant S\leqslant\frac{31}{8}$。
(ⅱ)当$\frac{7}{2}＜t＜4$时，矩形$O'C'D'E'$与$\triangle OAB$的重叠部分如图
(5)所示。

此时$AO' = OA - OO' = 4 - t = FO'$，$OE' = EE'-EO=t-\frac{7}{2}=ME'$。
易证$\triangle AO'F$和$\triangle OE'M$为等腰直角三角形，
∴$S_{\triangle AO'F}=\frac{1}{2}AO'\cdot FO'=\frac{1}{2}(4 - t)^{2}=\frac{1}{2}t^{2}-4t + 8$，
$S_{\triangle OE'M}=\frac{1}{2}OE'\cdot ME'=\frac{1}{2}(t-\frac{7}{2})^{2}=\frac{1}{2}t^{2}-\frac{7}{2}t+\frac{49}{8}$，
∴重叠部分面积$S = S_{\triangle AOB}-S_{\triangle OE'M}-S_{\triangle AO'F}=4-(\frac{1}{2}t^{2}-\frac{7}{2}t+\frac{49}{8})-(\frac{1}{2}t^{2}-4t + 8)=-t^{2}+\frac{15}{2}t-\frac{81}{8}$，
∴$S$是关于$t$的二次函数，且对称轴为直线$t=\frac{15}{4}$，开口向下，
∴自变量离对称轴越远，其对应的函数值越小，
∴将$t=\frac{15}{4}$代入，得最大值$S=-(\frac{15}{4})^{2}+\frac{15}{2}\times\frac{15}{4}-\frac{81}{8}=\frac{63}{16}$。
当$t = 4$时，$S=-4^{2}+\frac{15}{2}\times4-\frac{81}{8}=\frac{31}{8}$；当$t=\frac{7}{2}$时，$S=-(\frac{7}{2})^{2}+\frac{15}{2}\times\frac{7}{2}-\frac{81}{8}=\frac{31}{8}$，
∴当$\frac{7}{2}＜t＜4$时，$\frac{31}{8}＜S\leqslant\frac{63}{16}$。
(ⅲ)当$4\leqslant t\leqslant\frac{9}{2}$时，
由
(2)①可知$S=-\frac{1}{2}(t-\frac{7}{2})^{2}+4$。
∵$a=-\frac{1}{2}＜0$，
∴抛物线的开口向下，且对称轴为直线$t=\frac{7}{2}$，
∴在$4\leqslant t\leqslant\frac{9}{2}$范围内，当$t=\frac{9}{2}$时，$S$有最小值，为$S=-\frac{1}{2}\times(\frac{9}{2}-\frac{7}{2})^{2}+4=\frac{7}{2}$；当$t = 4$时，$S$有最大值，为$S=-\frac{1}{2}\times(4-\frac{7}{2})^{2}+4=\frac{31}{8}$。
∴当$4\leqslant t\leqslant\frac{9}{2}$时，$\frac{7}{2}\leqslant S\leqslant\frac{31}{8}$。
综上所述，$\frac{23}{8}\leqslant S\leqslant\frac{63}{16}$。
知识拓展：对于二次函数$y = a(x - h)^{2}+k$（$a$，$h$，$k$为常数，$a\neq0$），当$a＞0$时，抛物线开口向上，在对称轴的左侧$y$随$x$的增大而减小，在对称轴的右侧$y$随$x$的增大而增大，此时函数有最小值；当$a＜0$时，抛物线开口向下，在对称轴的左侧$y$随$x$的增大而增大，在对称轴的右侧$y$随$x$的增大而减小，此时函数有最大值。其顶点坐标是$(h,k)$，对称轴为直线$x = h$。