《2025年1课3练江苏人民出版社九年级数学下册北师大版》

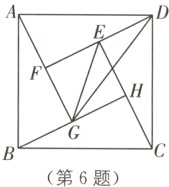
6 传统文化 赵爽弦图 (2024·达州 三模)勾股定理的证明方法丰富多样，其中我国古代数学家赵爽利用“弦图”的证明简明、直观，是世界公认最巧妙的方法. “赵爽弦图”已成为我国古代数学成就的一个重要标志，千百年来倍受人们的喜爱. 小亮在如图所示的“赵爽弦图”中，连接EG，DG. 若正方形ABCD与EFGH的边长之比为$\sqrt{5}$ : 1，则cos∠DGE等于( ).
A. $\frac{\sqrt{10}}{10}$ B. $\frac{\sqrt{2}}{5}$ C. $\frac{2\sqrt{5}}{5}$ D. $\frac{3\sqrt{10}}{10}$

答案：
6.D　[解析]如图,过点D作DN⊥GE,交GE的延长线于点N.
　设AF=BG=CH=DE=a,
　DF=AG=BH=CE=b,
　　　　　　　　　　　　　　
∵正方形ABCD与EFGH的边长之比为$\sqrt{5}$:1,
∴设正方形ABCD的边长为$\sqrt{5}$x,则正方形EFGH的边长为x.
∵AF²+DF²=AD²,DF−DE=EF,
∴$\begin{cases}a²+b²=(\sqrt{5}x)² \\ b - a = x \end{cases}$,解得$\begin{cases}b = 2x \\ a = x \end{cases}$,
∴AG=DF=b=2x,AF=a=x,
∴AG=2AF.
∵∠AFD=90°,
∴DF是AG的垂直平分线，
∴AD=DG=$\sqrt{5}$x.
∵∠EFG=90°,EF=FG=x,
∴EG=$\sqrt{EF²+FG²}$=$\sqrt{x²+x²}$=$\sqrt{2}$x,∠FEG=∠FGE=45°,
∴∠NED=∠FEG=45°.
　在Rt△END中,NE=DE·cos45°=$\frac{\sqrt{2}}{2}$x,
∴GN=EG+NE=$\sqrt{2}$x+$\frac{\sqrt{2}}{2}$x=$\frac{3\sqrt{2}}{2}$x.
　在Rt△DNG中,cos∠DGE=$\frac{NG}{DG}$=$\frac{\frac{3\sqrt{2}}{2}x}{\sqrt{5}x}$=$\frac{3\sqrt{10}}{10}$.故选D.

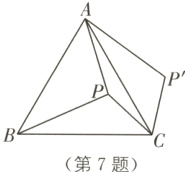
7 如图，点P在等边三角形ABC的内部，且PC = 6，PA = 8，PB = 10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，求sin∠PAP'的值.

答案： 7.连接PP′.
∵线段PC绕点C顺时针旋转60°得到P′C,
∴CP=CP′=6,∠PCP′=60°,
∴△CPP′为等边三角形，
∴PP′=PC=6.
∵△ABC为等边三角形，
∴CB=CA,∠ACB=60°,
∴∠PCB=∠P′CA.
　在△PCB和△P′CA中，$\begin{cases}PC = P′C \\ ∠PCB = ∠P′CA \\ CB = CA \end{cases}$,
∴△PCB≌△P′CA(SAS),
∴PB = P′A = 10.
∵6²+8²=10²,
∴PP′²+AP²=P′A².
∴△APP′为直角三角形，且∠APP′=90°，
∴sin∠PAP′=$\frac{PP′}{P′A}$=$\frac{6}{10}$=$\frac{3}{5}$.

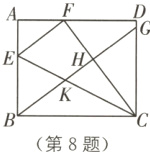
8 (2024·哈尔滨南岗区模拟)如图，在矩形ABCD中，点E，F分别在边AB，AD上，△EBC与△EFC关于直线EC对称，过点B作BH⊥FC于点H，交CE于点K，交CD于点G，tan∠FCB = $\frac{4}{3}$，若DG = $\frac{1}{2}$，则CE的长为______.

答案： 8.5$\sqrt{5}$　[解析]
∵△EBC与△EFC关于直线EC对称，
∴BE=EF,BC=CF,∠ABC=∠CFE=90°.
∵AD//BC,
∴∠BCF=∠DFC,
∴tan∠FCB=tan∠DFC=$\frac{CD}{FD}$=$\frac{4}{3}$,
∴设CD=4x,FD=3x,
∴FC=$\sqrt{FD²+CD²}$=5x=BC.
∵BH⊥FC,
∴∠FCB+∠GBC=90°=∠GBC+∠BGC,
∴∠BGC=∠FCB,
∴tan∠FCB=tan∠BGC=$\frac{BC}{GC}$=$\frac{4}{3}$,
∴$\frac{5x}{4x-\frac{1}{2}}=\frac{4}{3}$,解得x=2,
　经检验，x=2是原方程的解，
∴BC=FC=AD=10,DF=6,CD=8=AB,
∴AF=AD−DF=4.
∵∠AFE+∠DFC=90°=∠AFE+∠AEF,
∴∠AEF=∠DFC,
∴tan∠AEF=tan∠DFC=$\frac{AF}{AE}$=$\frac{4}{3}$,
∴AE=3,
∴BE=AB−AE=5.
　在Rt△BCE中,由勾股定理，得
　CE=$\sqrt{BE²+BC²}$=5$\sqrt{5}$.

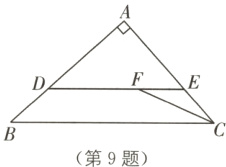
9 如图，在Rt△ABC中，∠BAC = 90°，点E在边AC上，AE = 2EC，过点E作DE//BC，交边AB于点D，CF平分∠ACB，交线段DE于点F. 若BC = 9，sin B = $\frac{2}{3}$，求DF的长.

答案： 9.
∵∠BAC=90°,BC=9,
∴sinB=$\frac{AC}{BC}$=$\frac{AC}{9}$=$\frac{2}{3}$,
∴AC=6.
∵AE=2EC,
∴AE=$\frac{2}{3}$AC=4,CE=$\frac{1}{3}$AC=2.
∵DE//BC,
∴∠ADE=∠B,
∴sin∠ADE=sinB=$\frac{2}{3}$,
∴$\frac{AE}{DE}$=$\frac{2}{3}$,
∴DE=6.
∵CF平分∠ACB，
∴∠BCF=∠ECF.
∵DE//BC,
∴∠BCF=∠EFC,
∴∠EFC=∠ECF,
∴EF=EC=2,
∴DF=DE−EF=6−2=4.

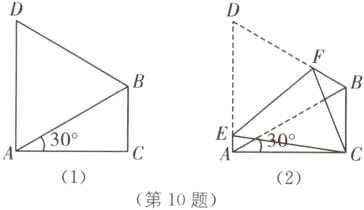
10 如图(1)，在△ABC中，∠ACB = 90°，∠CAB = 30°，△ABD是等边三角形. 如图(2)，将四边形ACBD折叠，使点D与点C重合，EF为折痕，求sin∠ACE的值.

答案： 10.在△ABC中,∠ACB=90°,∠BAC=30°,设BC=a,则AB=2a,AC=$\sqrt{AB²−BC²}$=$\sqrt{3}$a.
∵△ABD是等边三角形，
∴AD=AB=2a.
　设DE=EC=x,则AE=2a−x.
　在Rt△AEC中,由勾股定理,得(2a - x)²+($\sqrt{3}$a)²=x²,解得x=$\frac{7}{4}$a,
∴AE=$\frac{1}{4}$a,EC=$\frac{7}{4}$a.
∴sin∠ACE=$\frac{AE}{EC}$=$\frac{1}{7}$.