《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1 教材P39例1·改编 将二次函数$y = x^{2}-4x + 8$转化为$y = a(x - h)^{2}+k$的形式，其结果为( )．
A. $y=(x - 2)^{2}+4$
B. $y=(x + 4)^{2}+4$
C. $y=(x - 4)^{2}+8$
D. $y=(x - 2)^{2}-4$

答案： A

2 教材P41随堂练习·改编 把二次函数$y=-2x^{2}-4x + 5$用配方法化成$y = a(x - h)^{2}+k$的形式是______．

答案： y=−2(x + 1)²+7

3 二次函数$y = x^{2}+2x + 2$的图象的对称轴是直线( )．
A. $x=-1$
B. $x=-2$
C. $x = 1$
D. $x = 2$

答案： A

4 已知二次函数$y = ax^{2}+bx - c(a\neq0)$，其中$b＞0$，$c＞0$，则该函数的图象可能为( )．

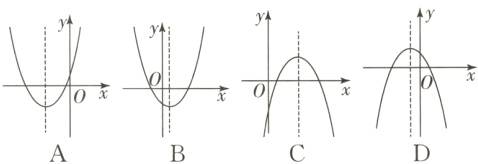
答案： C

5 教材P40做一做·改编 二次函数$y=-x^{2}-2x + 3$的图象的顶点坐标为______．

答案： (−1,4)

6 (2024·泸州中考)已知二次函数$y = ax^{2}+(2a - 3)x+a - 1$($x$是自变量)的图象经过第一、二、四象限，则实数$a$的取值范围为( )．
A. $1\leqslant a＜\frac{9}{8}$
B. $0 ＜ a＜\frac{3}{2}$
C. $0 ＜ a＜\frac{9}{8}$
D. $1\leqslant a＜\frac{3}{2}$

答案： A [解析]
∵二次函数y = ax²+(2a - 3)x + a - 1的图象经过第一、二、四象限，
∴抛物线开口向上，对称轴在y轴右侧，顶点在x轴下方，且与y轴的非负半轴相交，
∴a＞0，−$\frac{b}{2a}$=−$\frac{2a - 3}{2a}$＞0，解得0 ＜ a ＜ $\frac{3}{2}$，
$\frac{4ac - b²}{4a}$=$\frac{4a(a - 1)-(2a - 3)²}{4a}$＜0，解得0 ＜ a ＜ $\frac{9}{8}$，
a - 1≥0，解得a≥1，
∴a的取值范围为1≤a ＜ $\frac{9}{8}$. 故选A.
归纳总结 二次函数的一般式中，c确定图象与y轴的交点，当c＞0时，图象与y轴的正半轴相交；当c＜0时，图象与y轴的负半轴相交；当c = 0时，图象过原点. 再根据顶点所在象限，根据a确定开口方向，最终确定所过象限.

7 当$x\geqslant m$时，二次函数$y=-x^{2}+3x$的函数值$y$随$x$的增大而减小，则实数$m$的取值范围是______．

答案： m≥$\frac{3}{2}$

8 (教材P38议一议·变式)已知二次函数$y=-\frac{1}{2}x^{2}-x+\frac{7}{2}$．
(1)用配方法把该二次函数的表达式化为$y = a(x + m)^{2}+k$的形式；
(2)写出该二次函数图象的开口方向、顶点坐标和对称轴，并说明函数值$y$随自变量$x$的变化而变化的情况．

答案：
(1)y=−$\frac{1}{2}$x²−x+$\frac{7}{2}$=−$\frac{1}{2}$(x²+2x + 1)+$\frac{1}{2}$+$\frac{7}{2}$=−$\frac{1}{2}$(x + 1)²+4.
(2)①二次函数图象的开口向下；
②顶点坐标为(−1,4)；
③对称轴为直线x=−1；
④当x ＜ -1时，y随x的增大而增大；当x ＞ -1时，y随x的增大而减小.

9 (2023·东莞一模)将抛物线$y = x^{2}$向上平移2个单位，再向左平移1个单位，则平移后的抛物线表达式为( )．
A. $y = x^{2}+2x - 3$
B. $y = x^{2}-2x + 3$
C. $y = x^{2}+2x + 3$
D. $y = x^{2}-2x - 3$

答案： C

10 教材P41习题T2·改编 将抛物线$y = x^{2}-2x + 3$向左平移2个单位长度，所得抛物线为______．

答案： y=(x + 1)²+2

11 (2024·福建中考)已知二次函数$y = x^{2}-2ax + a$($a\neq0$)的图象经过$A(\frac{a}{2},y_{1})$，$B(3a,y_{2})$两点，则下列判断正确的是( )．
A. 可以找到一个实数$a$，使得$y_{1}＞a$
B. 无论实数$a$取什么值，都有$y_{1}＞a$
C. 可以找到一个实数$a$，使得$y_{2}＜0$
D. 无论实数$a$取什么值，都有$y_{2}＜0$

答案： C [解析]
∵二次函数表达式为y = x²−2ax + a（a≠0），
∴二次函数图象开口向上，且对称轴为直线x=−$\frac{-2a}{2}$=a，顶点坐标为(a,a - a²)，图象过点(0,a)，
当a＞0时，0 ＜ $\frac{a}{2}$ ＜ a，
∴a - a² ＜ y₁ ＜ a；
当a ＜ 0时，a ＜ $\frac{a}{2}$ ＜ 0，
∴a - a² ＜ y₁ ＜ a，
故A，B错误，不符合题意；
当a＞0时，0 ＜ a ＜ 2a ＜ 3a，由二次函数对称性可知点(0,a)和点(2a,a)关于对称轴对称，在对称轴右侧，y随x的增大而增大，
∴当x = 3a时，y₂＞a＞0；
当a ＜ 0时，3a ＜ 2a ＜ a ＜ 0，由二次函数对称性可知点(0,a)和点(2a,a)关于对称轴对称，在对称轴左侧，y随x的增大而减小，
∴当x = 3a时，y₂＞a，不一定大于0，故C正确，符合题意；D错误，不符合题意. 故选C.