2025年1课3练江苏人民出版社九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1课3练江苏人民出版社九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第63页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
3 (2023·牡丹江中考)将抛物线y=(x + 3)²向下平移1个单位长度,再向右平移______个单位长度后,得到的新抛物线经过原点。
答案:
2或4
4 二次函数y=ax²+bx+c图象上部分点的横纵坐标x,y的对应值如表:

(1)求二次函数的表达式和对称轴;
(2)表中的m=______,n=______;
(3)若P(-2024,y₁),Q(2025,y₂)是这个函数图象上的两点,则y₁______y₂(填“>”“=”或“<”);
(4)写出这个函数图象绕顶点旋转180°后的函数表达式:__________。

(1)求二次函数的表达式和对称轴;
(2)表中的m=______,n=______;
(3)若P(-2024,y₁),Q(2025,y₂)是这个函数图象上的两点,则y₁______y₂(填“>”“=”或“<”);
(4)写出这个函数图象绕顶点旋转180°后的函数表达式:__________。
答案:
(1)将$(-2,-4)$,$(-1,-3)$,$(0,-4)$代入$y = ax^{2}+bx + c$,
得$\begin{cases}4a - 2b + c = - 4\\a - b + c = - 3\\c = - 4\end{cases}$,解得$\begin{cases}a = - 1\\b = - 2\\c = - 4\end{cases}$,
$\therefore$二次函数的表达式为$y=-x^{2}-2x - 4=-(x + 1)^{2}-3$,$\therefore$对称轴为直线$x = - 1$。
(2)3 -12 [解析]由
(1)知函数表达式为$y=-x^{2}-2x - 4$,当$x = 2$时,$n = - 12$,
当$y = - 19$时,$-19=-x^{2}-2x - 4$,
解得$m = 3$或$-5$(舍去),$\therefore m = 3$。
(3)$\gt$ [解析]$\because$二次函数表达式为$y=-x^{2}-2x - 4$,$a = - 1\lt0$,$\therefore$图象开口向下,
$\therefore$自变量距离对称轴越远,对应的函数值越小。
$\because$对称轴为直线$x = - 1$,
$\therefore-1-(-2024)=2023$,$2025-(-1)=2026$。
$\because2023\lt2026$,$\therefore y_{1}\gt y_{2}$。
(4)$y=(x + 1)^{2}-3$ [解析]$\because y=-x^{2}-2x - 4=-(x + 1)^{2}-3$。
$\therefore$函数图象绕顶点旋转$180^{\circ}$后的函数表达式为$y=(x + 1)^{2}-3$。
(1)将$(-2,-4)$,$(-1,-3)$,$(0,-4)$代入$y = ax^{2}+bx + c$,
得$\begin{cases}4a - 2b + c = - 4\\a - b + c = - 3\\c = - 4\end{cases}$,解得$\begin{cases}a = - 1\\b = - 2\\c = - 4\end{cases}$,
$\therefore$二次函数的表达式为$y=-x^{2}-2x - 4=-(x + 1)^{2}-3$,$\therefore$对称轴为直线$x = - 1$。
(2)3 -12 [解析]由
(1)知函数表达式为$y=-x^{2}-2x - 4$,当$x = 2$时,$n = - 12$,
当$y = - 19$时,$-19=-x^{2}-2x - 4$,
解得$m = 3$或$-5$(舍去),$\therefore m = 3$。
(3)$\gt$ [解析]$\because$二次函数表达式为$y=-x^{2}-2x - 4$,$a = - 1\lt0$,$\therefore$图象开口向下,
$\therefore$自变量距离对称轴越远,对应的函数值越小。
$\because$对称轴为直线$x = - 1$,
$\therefore-1-(-2024)=2023$,$2025-(-1)=2026$。
$\because2023\lt2026$,$\therefore y_{1}\gt y_{2}$。
(4)$y=(x + 1)^{2}-3$ [解析]$\because y=-x^{2}-2x - 4=-(x + 1)^{2}-3$。
$\therefore$函数图象绕顶点旋转$180^{\circ}$后的函数表达式为$y=(x + 1)^{2}-3$。
5 已知抛物线y=x²+bx - 3(b是常数)经过点A(-1,0)。
(1)抛物线的表达式为______;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P',当点P'落在第二象限时,P'A²取得最小值时,求m的值。
(1)抛物线的表达式为______;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P',当点P'落在第二象限时,P'A²取得最小值时,求m的值。
答案:
(1)$y = x^{2}-2x - 3$ [解析]把$A(-1,0)$代入$y = x^{2}+bx - 3$,得$0 = 1 - b - 3$,解得$b = - 2$,即抛物线的表达式为$y = x^{2}-2x - 3$。
(2)由题意,可知$P'(-m,-t)$在第二象限,$P(m,t)$在第四象限,$\therefore m\gt0$,$t\lt0$。
$\because$抛物线的顶点坐标为$(1,-4)$,$\therefore-4\leqslant t\lt0$。
$\because$点$P$在抛物线上,$\therefore t = m^{2}-2m - 3$,
$\therefore m^{2}-2m=t + 3$。
$\because A(-1,0)$,$P'(-m,-t)$,
$\therefore P'A^{2}=(-m + 1)^{2}+(-t)^{2}=m^{2}-2m + 1 + t^{2}=t^{2}+t + 4=(t+\frac{1}{2})^{2}+\frac{15}{4}$,
$\therefore$当$t = -\frac{1}{2}$时,$P'A^{2}$有最小值,
$\therefore-\frac{1}{2}=m^{2}-2m - 3$,
解得$m=\frac{2-\sqrt{14}}{2}$或$m=\frac{2+\sqrt{14}}{2}$。
$\because m\gt0$,$\therefore m=\frac{2-\sqrt{14}}{2}$不合题意,舍去,
$\therefore m$的值为$\frac{2+\sqrt{14}}{2}$。
(1)$y = x^{2}-2x - 3$ [解析]把$A(-1,0)$代入$y = x^{2}+bx - 3$,得$0 = 1 - b - 3$,解得$b = - 2$,即抛物线的表达式为$y = x^{2}-2x - 3$。
(2)由题意,可知$P'(-m,-t)$在第二象限,$P(m,t)$在第四象限,$\therefore m\gt0$,$t\lt0$。
$\because$抛物线的顶点坐标为$(1,-4)$,$\therefore-4\leqslant t\lt0$。
$\because$点$P$在抛物线上,$\therefore t = m^{2}-2m - 3$,
$\therefore m^{2}-2m=t + 3$。
$\because A(-1,0)$,$P'(-m,-t)$,
$\therefore P'A^{2}=(-m + 1)^{2}+(-t)^{2}=m^{2}-2m + 1 + t^{2}=t^{2}+t + 4=(t+\frac{1}{2})^{2}+\frac{15}{4}$,
$\therefore$当$t = -\frac{1}{2}$时,$P'A^{2}$有最小值,
$\therefore-\frac{1}{2}=m^{2}-2m - 3$,
解得$m=\frac{2-\sqrt{14}}{2}$或$m=\frac{2+\sqrt{14}}{2}$。
$\because m\gt0$,$\therefore m=\frac{2-\sqrt{14}}{2}$不合题意,舍去,
$\therefore m$的值为$\frac{2+\sqrt{14}}{2}$。
6 中考新考法 存在性问题探究 如图(1),抛物线y=-x²+bx+3与x轴交于点A,B,与y轴交于点C,点B坐标为(6,0),点D为线段OB上一点,点E为抛物线上一动点。
(1)求b的值。
(2)点D坐标为(3,0),点E在第一象限的抛物线上,设△ECD的面积为S,求S的最大值。
(3)如图(2),点D坐标为(4,0),是否存在点E,使∠ABE=∠ODC,若存在,请求出点E坐标;若不存在,说明理由。
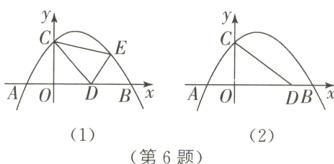
(1)求b的值。
(2)点D坐标为(3,0),点E在第一象限的抛物线上,设△ECD的面积为S,求S的最大值。
(3)如图(2),点D坐标为(4,0),是否存在点E,使∠ABE=∠ODC,若存在,请求出点E坐标;若不存在,说明理由。

答案:
(1)将点$B(6,0)$代入抛物线函数表达式,
得$0=-36 + 6b + 3$,解得$b=\frac{11}{2}$。
(2)由
(1)知,抛物线的函数表达式为$y=-x^{2}+\frac{11}{2}x + 3$ ①,由抛物线的函数表达式知$OC = 3$。
如图,过点$E$分别作$x$轴,$y$轴的垂线,垂足分别为$H$,$N$,连接$OE$。
设点$E$坐标为$(x,-x^{2}+\frac{11}{2}x + 3)$,
则$S = S_{四边形OCED}-S_{\triangle OCD}=\frac{1}{2}OC\cdot NE+\frac{1}{2}OD\cdot EH-\frac{1}{2}\times3\times3=\frac{1}{2}\times3\times x+\frac{1}{2}\times3\times(-x^{2}+\frac{11}{2}x + 3)-\frac{9}{2}=-\frac{3}{2}x^{2}+\frac{39}{4}x$。$\because-\frac{3}{2}\lt0$,$\therefore S$有最大值。当$x=\frac{13}{4}$时,$S$的最大值为$\frac{507}{32}$。
(3)由点$C$,$D$的坐标,得直线$CD$的函数表达式为$y = -\frac{3}{4}x + 3$。
当点$E$在$x$轴上方时,
$\because\angle ABE=\angle ODC$,$\therefore BE// CD$,$\therefore$直线$BE$的函数表达式为$y = -\frac{3}{4}(x - 6)$②。
联立①②,得$-\frac{3}{4}(x - 6)=-x^{2}+\frac{11}{2}x + 3$,
解得$x = 6$(舍去)或$x=\frac{1}{4}$,故点$E$坐标为$(\frac{1}{4},\frac{69}{16})$;
当点$E$在$x$轴下方时,根据函数的对称性,则直线$BE$的函数表达式为$y=\frac{3}{4}(x - 6)$③,
联立①③,得$\frac{3}{4}(x - 6)=-x^{2}+\frac{11}{2}x + 3$,
解得$x = 6$(舍去)或$-\frac{5}{4}$,
故点$E$坐标为$(-\frac{5}{4},-\frac{87}{16})$。
综上,点$E$的坐标为$(\frac{1}{4},\frac{69}{16})$或$(-\frac{5}{4},-\frac{87}{16})$。
(1)将点$B(6,0)$代入抛物线函数表达式,
得$0=-36 + 6b + 3$,解得$b=\frac{11}{2}$。
(2)由
(1)知,抛物线的函数表达式为$y=-x^{2}+\frac{11}{2}x + 3$ ①,由抛物线的函数表达式知$OC = 3$。
如图,过点$E$分别作$x$轴,$y$轴的垂线,垂足分别为$H$,$N$,连接$OE$。
设点$E$坐标为$(x,-x^{2}+\frac{11}{2}x + 3)$,
则$S = S_{四边形OCED}-S_{\triangle OCD}=\frac{1}{2}OC\cdot NE+\frac{1}{2}OD\cdot EH-\frac{1}{2}\times3\times3=\frac{1}{2}\times3\times x+\frac{1}{2}\times3\times(-x^{2}+\frac{11}{2}x + 3)-\frac{9}{2}=-\frac{3}{2}x^{2}+\frac{39}{4}x$。$\because-\frac{3}{2}\lt0$,$\therefore S$有最大值。当$x=\frac{13}{4}$时,$S$的最大值为$\frac{507}{32}$。
(3)由点$C$,$D$的坐标,得直线$CD$的函数表达式为$y = -\frac{3}{4}x + 3$。
当点$E$在$x$轴上方时,
$\because\angle ABE=\angle ODC$,$\therefore BE// CD$,$\therefore$直线$BE$的函数表达式为$y = -\frac{3}{4}(x - 6)$②。
联立①②,得$-\frac{3}{4}(x - 6)=-x^{2}+\frac{11}{2}x + 3$,
解得$x = 6$(舍去)或$x=\frac{1}{4}$,故点$E$坐标为$(\frac{1}{4},\frac{69}{16})$;
当点$E$在$x$轴下方时,根据函数的对称性,则直线$BE$的函数表达式为$y=\frac{3}{4}(x - 6)$③,
联立①③,得$\frac{3}{4}(x - 6)=-x^{2}+\frac{11}{2}x + 3$,
解得$x = 6$(舍去)或$-\frac{5}{4}$,
故点$E$坐标为$(-\frac{5}{4},-\frac{87}{16})$。
综上,点$E$的坐标为$(\frac{1}{4},\frac{69}{16})$或$(-\frac{5}{4},-\frac{87}{16})$。
查看更多完整答案,请扫码查看


