2025年1课3练江苏人民出版社九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1课3练江苏人民出版社九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第60页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
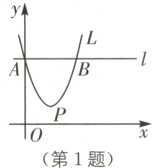
1 (2024·河北邯郸期中)如图,在平面直角坐标系中,抛物线L:$y = ax^{2}-2ax+\frac{8}{3}$与y轴交于点A,过点A作x轴的平行线l交抛物线于点B,P为抛物线的顶点.
(1)抛物线L的对称轴为直线x = ________;
(2)连接OP并延长交直线l于点Q.若点B恰为线段AQ的中点,则a的值为________.
(1)抛物线L的对称轴为直线x = ________;
(2)连接OP并延长交直线l于点Q.若点B恰为线段AQ的中点,则a的值为________.

答案:
(1)1 [解析]
∵抛物线为$y = ax^{2}-2ax+\frac{8}{3}$,
∴对称轴为直线$x = -\frac{-2a}{2a}=1$.
(2)2 [解析]
∵抛物线$y = ax^{2}-2ax+\frac{8}{3}(a>0)$与$y$轴交于点$A$,
∴$A(0,\frac{8}{3})$,抛物线的对称轴为直线$x = 1$.
∴顶点$P$坐标为$(1,\frac{8}{3}-a)$,点$B$坐标为$(2,\frac{8}{3})$.
∵点$B$为线段$AQ$的中点,
∴点$Q$的坐标为$(4,\frac{8}{3})$.
设直线$OP$表达式为$y = kx$($k$为常数,且$k\neq0$),
将点$P(1,\frac{8}{3}-a)$代入,得$\frac{8}{3}-a = k$,
∴$y = (\frac{8}{3}-a)x$.
将点$Q(4,\frac{8}{3})$代入,得$\frac{8}{3}=(\frac{8}{3}-a)\times4$,解得$a = 2$.
(1)1 [解析]
∵抛物线为$y = ax^{2}-2ax+\frac{8}{3}$,
∴对称轴为直线$x = -\frac{-2a}{2a}=1$.
(2)2 [解析]
∵抛物线$y = ax^{2}-2ax+\frac{8}{3}(a>0)$与$y$轴交于点$A$,
∴$A(0,\frac{8}{3})$,抛物线的对称轴为直线$x = 1$.
∴顶点$P$坐标为$(1,\frac{8}{3}-a)$,点$B$坐标为$(2,\frac{8}{3})$.
∵点$B$为线段$AQ$的中点,
∴点$Q$的坐标为$(4,\frac{8}{3})$.
设直线$OP$表达式为$y = kx$($k$为常数,且$k\neq0$),
将点$P(1,\frac{8}{3}-a)$代入,得$\frac{8}{3}-a = k$,
∴$y = (\frac{8}{3}-a)x$.
将点$Q(4,\frac{8}{3})$代入,得$\frac{8}{3}=(\frac{8}{3}-a)\times4$,解得$a = 2$.
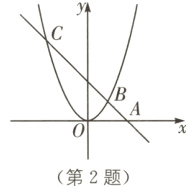
2 中考新考法 存在性问题 如图,直线AB过x轴上的点A(2,0),且与抛物线$y = ax^{2}$相交于B,C两点,点B的坐标为(1,1).
(1)求直线AB和抛物线的函数表达式.
(2)在抛物线上是否存在一点D,使$S_{\triangle OAD}=S_{\triangle OBC}$?若不存在,请说明理由;若存在,请求出点D的坐标.
(1)求直线AB和抛物线的函数表达式.
(2)在抛物线上是否存在一点D,使$S_{\triangle OAD}=S_{\triangle OBC}$?若不存在,请说明理由;若存在,请求出点D的坐标.

答案:
(1)直线$AB$的表达式为$y = -x + 2$,
抛物线的表达式为$y = x^{2}$.
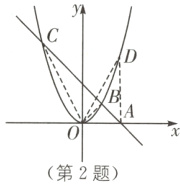
(2)如图,假设存在点$D(x,x^{2})$,使得$S_{\triangle OAD}=S_{\triangle OBC}$,
∴$S_{\triangle OAD}=\frac{1}{2}|OA|\cdot|y_{D}|=\frac{1}{2}\times2\times x^{2}=x^{2}$.
∵直线$AB$与抛物线交于点$C$,$B$,联立,得$\begin{cases}y = -x + 2\\y = x^{2}\end{cases}$,
解得$\begin{cases}x_{1}=1\\y_{1}=1\end{cases}$或$\begin{cases}x_{2}=-2\\y_{2}=4\end{cases}$.
∵$B(1,1)$,
∴$C(-2,4)$.
∴$S_{\triangle BOC}=S_{\triangle AOC}-S_{\triangle AOB}$
$=\frac{1}{2}\times2\times4-\frac{1}{2}\times2\times1 = 3$.
∵$S_{\triangle BOC}=S_{\triangle OAD}$,
∴$x^{2}=3$,
解得$x = \pm\sqrt{3}$.
∴点$D$的坐标为$(-\sqrt{3},3)$或$(\sqrt{3},3)$.
(1)直线$AB$的表达式为$y = -x + 2$,
抛物线的表达式为$y = x^{2}$.
(2)如图,假设存在点$D(x,x^{2})$,使得$S_{\triangle OAD}=S_{\triangle OBC}$,
∴$S_{\triangle OAD}=\frac{1}{2}|OA|\cdot|y_{D}|=\frac{1}{2}\times2\times x^{2}=x^{2}$.
∵直线$AB$与抛物线交于点$C$,$B$,联立,得$\begin{cases}y = -x + 2\\y = x^{2}\end{cases}$,

解得$\begin{cases}x_{1}=1\\y_{1}=1\end{cases}$或$\begin{cases}x_{2}=-2\\y_{2}=4\end{cases}$.
∵$B(1,1)$,
∴$C(-2,4)$.
∴$S_{\triangle BOC}=S_{\triangle AOC}-S_{\triangle AOB}$
$=\frac{1}{2}\times2\times4-\frac{1}{2}\times2\times1 = 3$.
∵$S_{\triangle BOC}=S_{\triangle OAD}$,
∴$x^{2}=3$,
解得$x = \pm\sqrt{3}$.
∴点$D$的坐标为$(-\sqrt{3},3)$或$(\sqrt{3},3)$.
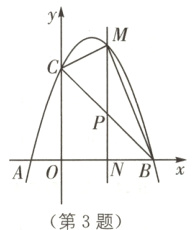
3 如图,已知抛物线$y = ax^{2}+bx + 3$与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,连接BC.
(1)求抛物线的函数表达式.
(2)若点P为线段BC上的一动点(不与B,C重合),过点P作PM//y轴,交抛物线于点M,交x轴于点N,当$\triangle BCM$的面积最大时,求点P的坐标.
(3)在(2)的条件下,当$\triangle BCM$的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A,P,D,E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
(1)求抛物线的函数表达式.
(2)若点P为线段BC上的一动点(不与B,C重合),过点P作PM//y轴,交抛物线于点M,交x轴于点N,当$\triangle BCM$的面积最大时,求点P的坐标.
(3)在(2)的条件下,当$\triangle BCM$的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A,P,D,E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.

答案:
(1)依题意,得$\begin{cases}a - b + 3 = 0\\9a + 3b + 3 = 0\end{cases}$,解得$\begin{cases}a = -1\\b = 2\end{cases}$,
∴抛物线的函数表达式为$y = -x^{2}+2x + 3$.
(2)设直线$BC$的表达式为$y = kx + m$,将点$B(3,0)$,$C(0,3)$代入,得$\begin{cases}3k + m = 0\\m = 3\end{cases}$,解得$\begin{cases}k = -1\\m = 3\end{cases}$,
∴直线$BC$的表达式为$y = -x + 3$.
设点$P$的坐标为$(t,-t + 3)$,则点$M$的坐标为$(t,-t^{2}+2t + 3)$,
∴$PM = -t^{2}+2t + 3 + t - 3 = -t^{2}+3t$,
∴$S_{\triangle BCM}=S_{\triangle PMC}+S_{\triangle PMB}=\frac{1}{2}PM\cdot OB=\frac{1}{2}(-t^{2}+3t)\times3 = -\frac{3}{2}(t - \frac{3}{2})^{2}+\frac{27}{8}$,
∴当$t = \frac{3}{2}$时,$\triangle BCM$的面积最大,此时,点$P$的坐标为$(\frac{3}{2},\frac{3}{2})$.
(3)
∵$y = -x^{2}+2x + 3 = -(x - 1)^{2}+4$,
∴对称轴为直线$x = 1$.
当四边形$APDE$为平行四边形时,$AP// ED$,$AP = ED$.
∵$A(-1,0)$,$P(\frac{3}{2},\frac{3}{2})$,
∴$x_{A}-x_{P}=x_{E}-x_{D}=-1-\frac{3}{2}=-\frac{5}{2}$.
∵$x_{D}=1$,
∴$x_{E}=-\frac{3}{2}$,
∴$E(-\frac{3}{2},-\frac{9}{4})$;
当四边形$APED$为平行四边形时,$AP// DE$,$AP = DE$,
∴$x_{A}-x_{P}=x_{D}-x_{E}=-1-\frac{3}{2}=-\frac{5}{2}$.
∵$x_{D}=1$,
∴$x_{E}=\frac{7}{2}$,
∴$E(\frac{7}{2},-\frac{9}{4})$;
当四边形$ADPE$为平行四边形时,$AE// DP$,$AE = DP$,
∴$x_{A}+x_{P}=x_{D}+x_{E}=-1+\frac{3}{2}=\frac{1}{2}$.
∵$x_{D}=1$,
∴$x_{E}=-\frac{1}{2}$,
∴$E(-\frac{1}{2},\frac{7}{4})$.
∴存在点$E$,使得以$A$,$P$,$D$,$E$为顶点的四边形为平行四边形,点$E$的坐标是$(-\frac{3}{2},-\frac{9}{4})$或$(\frac{7}{2},-\frac{9}{4})$或$(-\frac{1}{2},\frac{7}{4})$.
(1)依题意,得$\begin{cases}a - b + 3 = 0\\9a + 3b + 3 = 0\end{cases}$,解得$\begin{cases}a = -1\\b = 2\end{cases}$,
∴抛物线的函数表达式为$y = -x^{2}+2x + 3$.
(2)设直线$BC$的表达式为$y = kx + m$,将点$B(3,0)$,$C(0,3)$代入,得$\begin{cases}3k + m = 0\\m = 3\end{cases}$,解得$\begin{cases}k = -1\\m = 3\end{cases}$,
∴直线$BC$的表达式为$y = -x + 3$.
设点$P$的坐标为$(t,-t + 3)$,则点$M$的坐标为$(t,-t^{2}+2t + 3)$,
∴$PM = -t^{2}+2t + 3 + t - 3 = -t^{2}+3t$,
∴$S_{\triangle BCM}=S_{\triangle PMC}+S_{\triangle PMB}=\frac{1}{2}PM\cdot OB=\frac{1}{2}(-t^{2}+3t)\times3 = -\frac{3}{2}(t - \frac{3}{2})^{2}+\frac{27}{8}$,
∴当$t = \frac{3}{2}$时,$\triangle BCM$的面积最大,此时,点$P$的坐标为$(\frac{3}{2},\frac{3}{2})$.
(3)
∵$y = -x^{2}+2x + 3 = -(x - 1)^{2}+4$,
∴对称轴为直线$x = 1$.
当四边形$APDE$为平行四边形时,$AP// ED$,$AP = ED$.
∵$A(-1,0)$,$P(\frac{3}{2},\frac{3}{2})$,
∴$x_{A}-x_{P}=x_{E}-x_{D}=-1-\frac{3}{2}=-\frac{5}{2}$.
∵$x_{D}=1$,
∴$x_{E}=-\frac{3}{2}$,
∴$E(-\frac{3}{2},-\frac{9}{4})$;
当四边形$APED$为平行四边形时,$AP// DE$,$AP = DE$,
∴$x_{A}-x_{P}=x_{D}-x_{E}=-1-\frac{3}{2}=-\frac{5}{2}$.
∵$x_{D}=1$,
∴$x_{E}=\frac{7}{2}$,
∴$E(\frac{7}{2},-\frac{9}{4})$;
当四边形$ADPE$为平行四边形时,$AE// DP$,$AE = DP$,
∴$x_{A}+x_{P}=x_{D}+x_{E}=-1+\frac{3}{2}=\frac{1}{2}$.
∵$x_{D}=1$,
∴$x_{E}=-\frac{1}{2}$,
∴$E(-\frac{1}{2},\frac{7}{4})$.
∴存在点$E$,使得以$A$,$P$,$D$,$E$为顶点的四边形为平行四边形,点$E$的坐标是$(-\frac{3}{2},-\frac{9}{4})$或$(\frac{7}{2},-\frac{9}{4})$或$(-\frac{1}{2},\frac{7}{4})$.
4 (2024·江门鹤山一模)抛物线P:$y = ax^{2}+bx+\frac{3}{2}$与x轴交于点A(-1,0),B(3,0),与y轴交于点C,顶点为D.
(1)求抛物线P的函数表达式和顶点D的坐标.
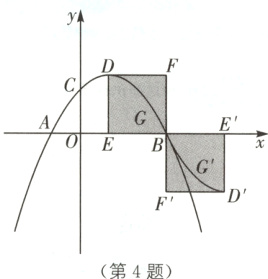
(2)如图,在坐标平面上放置一透明矩形胶片DEBF,并在胶片上描画出抛物线P在矩形胶片内部(含边界)的一段,记为G,把该胶片绕点B顺时针旋转180°,得到矩形胶片D'E'B F'以及对应的图象G'.
①求旋转过程中G扫过的面积S;
②求图象G'所在的抛物线的函数表达式.
(1)求抛物线P的函数表达式和顶点D的坐标.
(2)如图,在坐标平面上放置一透明矩形胶片DEBF,并在胶片上描画出抛物线P在矩形胶片内部(含边界)的一段,记为G,把该胶片绕点B顺时针旋转180°,得到矩形胶片D'E'B F'以及对应的图象G'.
①求旋转过程中G扫过的面积S;
②求图象G'所在的抛物线的函数表达式.

答案:
(1)把点$A(-1,0)$,$B(3,0)$代入$y = ax^{2}+bx+\frac{3}{2}$,
得$\begin{cases}a - b+\frac{3}{2}=0\\9a + 3b+\frac{3}{2}=0\end{cases}$,解得$\begin{cases}a = -\frac{1}{2}\\b = 1\end{cases}$,
∴抛物线$P$的函数表达式为$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}$.
∵$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}=-\frac{1}{2}(x - 1)^{2}+2$,
∴抛物线$P$的顶点$D$的坐标为$(1,2)$.
(2)①如图,连接$BD$,$BD'$.
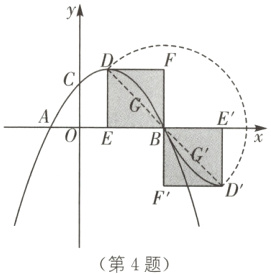
由$B(3,0)$,$D(1,2)$,得$BE = OB - OE = 3 - 1 = 2$,$DE = 2$.
在$Rt\triangle BED$中,$BD^{2}=BE^{2}+DE^{2}=2^{2}+2^{2}=8$.
由旋转性质可知,$BD$与$G$围成的图形,和$BD'$与$G'$围成的图形全等,二者面积相等,
∴旋转过程中$G$扫过的面积,即图中$G$,$G'$与半圆围成的图形面积,等于以$DD'$为直径的半圆的面积,
∴$S=\frac{1}{2}\pi\cdot BD^{2}=\frac{1}{2}\pi\times8 = 4\pi$.
②由旋转性质可知,$D'E' = DE = 2$,$BE' = BE = 2$,
∴$OE' = OB + BE' = 3 + 2 = 5$,
∴点$D'$的坐标为$(5,-2)$.
设图象$G'$所在抛物线的函数表达式为$y = m(x - 5)^{2}-2$,代入点$B(3,0)$,得$4m - 2 = 0$,解得$m = \frac{1}{2}$,
∴图象$G'$所在抛物线的函数表达式为$y = \frac{1}{2}(x - 5)^{2}-2(3\leqslant x\leqslant5)$.
(1)把点$A(-1,0)$,$B(3,0)$代入$y = ax^{2}+bx+\frac{3}{2}$,
得$\begin{cases}a - b+\frac{3}{2}=0\\9a + 3b+\frac{3}{2}=0\end{cases}$,解得$\begin{cases}a = -\frac{1}{2}\\b = 1\end{cases}$,
∴抛物线$P$的函数表达式为$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}$.
∵$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}=-\frac{1}{2}(x - 1)^{2}+2$,
∴抛物线$P$的顶点$D$的坐标为$(1,2)$.
(2)①如图,连接$BD$,$BD'$.

由$B(3,0)$,$D(1,2)$,得$BE = OB - OE = 3 - 1 = 2$,$DE = 2$.
在$Rt\triangle BED$中,$BD^{2}=BE^{2}+DE^{2}=2^{2}+2^{2}=8$.
由旋转性质可知,$BD$与$G$围成的图形,和$BD'$与$G'$围成的图形全等,二者面积相等,
∴旋转过程中$G$扫过的面积,即图中$G$,$G'$与半圆围成的图形面积,等于以$DD'$为直径的半圆的面积,
∴$S=\frac{1}{2}\pi\cdot BD^{2}=\frac{1}{2}\pi\times8 = 4\pi$.
②由旋转性质可知,$D'E' = DE = 2$,$BE' = BE = 2$,
∴$OE' = OB + BE' = 3 + 2 = 5$,
∴点$D'$的坐标为$(5,-2)$.
设图象$G'$所在抛物线的函数表达式为$y = m(x - 5)^{2}-2$,代入点$B(3,0)$,得$4m - 2 = 0$,解得$m = \frac{1}{2}$,
∴图象$G'$所在抛物线的函数表达式为$y = \frac{1}{2}(x - 5)^{2}-2(3\leqslant x\leqslant5)$.
查看更多完整答案,请扫码查看


