《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1 (2024·浙江宁波北仑区期末)某超市销售一种饮料，每瓶进价为4元，经市场调查表明：每瓶售价每增加1元，日均销售量减少80瓶；当售价为每瓶7元时，日均销售量为400瓶，若要日均毛利润最大，则每瓶饮料的售价应是( )．
A. 6元
B. 7元
C. 8元
D. 9元

答案： C

2 (2024·河北石家庄四十二中期末)某商店购进一批单价为20元的商品，若以单价30元销售，则每月可售出400件，如果销售单价每提高1元，那么月销售量相应减少20件，设每件商品单价涨x元，月销售利润为y元，可列函数为y=(30+x - 20)(400 - 20x). 对所列函数下列说法错误的是( )．
A. (30+x - 20)表示涨价后商品的单价
B. 20x表示涨价后少售出商品的数量
C. (400 - 20x)表示涨价后商品的月销售量
D. 当x = 5时月销售利润达到最大

答案： A

3 教材P56习题T2·变式(2024·天津红桥区三模)某服装店试销一种成本为每件60元的服装，规定试销期间每件服装的销售单价不低于成本，且获得的利润不得高于成本的45%. 经试销发现，销售量y(件)与销售单价x(元)符合一次函数关系y = - x + 120. 有下列结论：①销售单价可以是90元；②该服装店销售这种服装可获得的最大利润为891元；③销售单价有两个不同的值满足该服装店销售这种服装获得的利润为500元. 其中，正确结论的个数是( )．
A. 0
B. 1
C. 2
D. 3

答案： B [解析]
∵销售单价不低于成本，且每件服装获利不得高于成本的45%，
∴0≤x - 60≤60×45%，
∴60≤x≤87，　故①错误，不符合题意;　设服装店销售这种服装可获得的利润为w元，　则w=(x - 60)·(-x + 120)　=-x² + 180x - 7200=-(x - 90)² + 900.
∵-1＜0，
∴当x＜90时，w随x的增大而增大.
∵60≤x≤87，
∴当x = 87时，w最大，最大值为-(87 - 90)² + 900=891，故②正确，符合题意;　当w = 500时，则(x - 60)·(-x + 120)=500，　解得x₁ = 70，x₂ = 110(不合题意，舍去).
∴销售单价应定为70元，故③错误，不符合题意.　故正确结论的个数为1.故选B.

4 教材P49随堂练习·改编 某书店购进了一批单价为20元的中华传统文化丛书. 在销售的过程中发现，这种图书每天的销售数量y(本)与销售单价x(元)满足一次函数关系：y = - 3x + 108(29≤x≤36). 如果销售这种图书每天的利润为p(元)，那么在这种关系下销售单价定为________元时，每天获得的利润最大.

答案： 29

5 (2024·新疆中考)某公司销售一批产品，经市场调研发现，当销售量在0.4吨至3.5吨之间时，销售额y₁(万元)与销售量x(吨)的函数表达式为y₁ = 5x；成本y₂(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分，其中(1/2, 7/4)是其顶点.
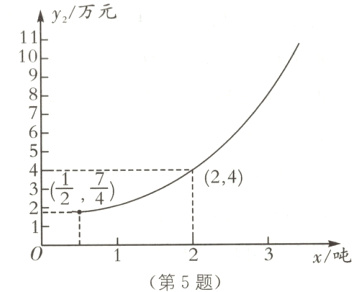
(1)求出成本y₂关于销售量x的函数表达式.
(2)当成本最低时，销售产品所获利润是多少?
(3)当销售量是多少吨时，可获得最大利润? 最大利润是多少?
(注：利润 = 销售额 - 成本)

答案：
(1)由抛物线的顶点为($\frac{1}{2}$,$\frac{7}{4}$)，　可设抛物线为y₂=a$(x - \frac{1}{2})² + \frac{7}{4}$.
∵抛物线过(2,4)，
∴a×$(2 - \frac{1}{2})² + \frac{7}{4}=4$，　解得a = 1，
∴y₂=$(x - \frac{1}{2})² + \frac{7}{4}$.　
(2)由题意，得当销售量x=$\frac{1}{2}$时，成本最低为$\frac{7}{4}$万元，且销售量在0.4吨至3.5吨之间时，销售额y₁(万元)　与销售量x(吨)的函数表达式为y₁ = 5x，
∴当x = $\frac{1}{2}$时，销售额为y₁ = 5x = 5×$\frac{1}{2}$ = 2.5(万元)，
∴此时利润为2.5 - $\frac{7}{4}$ = 0.75(万元).　故当成本最低时，销售产品所获利润是0.75万元.　
(3)由题意，得利润=y₁ - y₂ = 5x - $[(x - \frac{1}{2})² + \frac{7}{4}]$　=-x² + 6x - 2=-(x - 3)² + 7.
∵-1＜0，
∴当x = 3时，利润取最大值，最大值为7.故当销售量是3吨时，可获得最大利润，最大利润是7万元.