《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1 (2024·聊城模拟)如图，在Rt△ABC中，∠ACB = 90°，CD是中线，过点A作CD的垂线，分别交BC，CD于点E，F. 若tan∠CAE = $\frac{2}{3}$，AE = 26，则CD的长为( ).
A. 39 B. $8\sqrt{13}$ C. $6\sqrt{13}$ D. 19.5

答案： 1.D　[解析]在Rt△ACE中,tan∠CAE=$\frac{CE}{AC}$=$\frac{2}{3}$,
∴设CE=2x,则AC=3x,
∴(2x)²+(3x)²=26²,解得x=2$\sqrt{13}$(负值舍去)，
∴AC=6$\sqrt{13}$
∵∠ACB=90°,
∴∠CAE+∠AEC=90°.
　又∠AEC+∠ECD=90°,
∴∠CAE=∠ECD.
∵CD是斜边AB上的中线，
∴CD=BD,
∴∠ECD=∠B,
∴∠CAE=∠B,
∴tanB=tan∠CAE=$\frac{2}{3}$.
　在Rt△ABC中,tanB=$\frac{AC}{BC}$，
∴BC=$\frac{6\sqrt{13}}{\frac{2}{3}}$=9$\sqrt{13}$
∴AB=$\sqrt{(6\sqrt{13})²+(9\sqrt{13})²}$=39,
∴CD=$\frac{1}{2}$AB=19.5.故选D

2 中考新考法 满足条件的结论开放 学过三角函数之后，小明同学明白了梯子的倾斜程度和∠BAC的三角函数值有关. 如图，墙壁BC的高度是4 m，若梯子AB的坡度i满足1 : 1≤i≤5 : 1，则梯子AB的长度可以为______m. (AB的长度用有理数表示，精确到0.1)

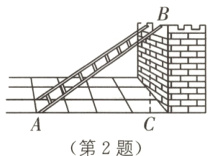
答案： 2.5.1(答案不唯一)

3 (2024·浙江金华义乌期末)如图，在等腰三角形ABC中，AB = BC = 5，sin∠ABD = $\frac{4}{5}$，过点A作AD⊥BC于点D.
(1)求BD的长；
(2)若E是边AC的中点，连接BE，求tan∠EBC的值.

答案： 3.
(1)
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
　在Rt△ABD中,AB=5,sin∠ABD=$\frac{AD}{AB}$=$\frac{4}{5}$,
∴AD=5×$\frac{4}{5}$=4,
∴BD=$\sqrt{5²−4²}$=3.
(2)
∵BC=5,BD=3,
∴CD=2.
∵AB=BC,且E是边AC的中点，
∴BE⊥AC,
∴∠EBC+∠C=90°.
∵∠CAD+∠C=90°,
∴∠EBC=∠CAD.
　在Rt△CAD中,tan∠CAD=$\frac{CD}{AD}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴tan∠EBC=$\frac{1}{2}$.

4 如图，在矩形ABCD中，AB = 6，BC = 8，点E在DC上，把△ADE沿AE折叠，点D恰好落在边BC上的点F处，求cos∠CEF的值.

答案： 4.
∵四边形ABCD是矩形，
∴AD=BC=8,DC=AB=6.
∵把△ADE沿AE折叠，点D恰好落在边BC上的点F处，
∴AF=AD=8,EF=DE,
∴BF=$\sqrt{AF²−AB²}$=$\sqrt{8²−6²}$=2$\sqrt{7}$,
∴CF=BC−BF=8−2$\sqrt{7}$
　在Rt△EFC中,CE=DC−DE=6−EF,
　由勾股定理,得EF²=CE²+CF²，
∴EF²=(6−EF)²+(8−2$\sqrt{7}$)²,
∴EF=$\frac{32−8\sqrt{7}}{3}$,
∴CE=6−$\frac{32−8\sqrt{7}}{3}$=$\frac{8\sqrt{7}−14}{3}$,
∴cos∠CEF=$\frac{CE}{EF}$=$\frac{\frac{8\sqrt{7}-14}{3}}{\frac{32 - 8\sqrt{7}}{3}}=\frac{\sqrt{7}}{4}$.
　一题多解
　
∵四边形ABCD是矩形，
∴AD=BC=8,∠B=∠C=∠D=90°,
∴∠FEC+∠EFC=90°,
∵把△ADE沿AE折叠，点D恰好落在边BC上的点F处，
∴AF=AD=8,∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,
∴∠FEC=∠AFB,
∵AB=6,
∴BF=$\sqrt{AF²−AB²}$=$\sqrt{8²−6²}$=2$\sqrt{7}$,
∴cos∠CEF=cos∠AFB = $\frac{BF}{AF}=\frac{2\sqrt{7}}{8}=\frac{\sqrt{7}}{4}$.

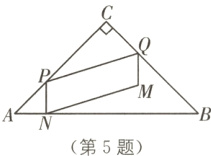
5 如图，在Rt△ABC中，∠C = 90°，AC = BC = 4$\sqrt{2}$. 点P从点A出发，沿AC向终点C运动，同时点Q从点C出发，沿CB运动，它们的速度均为每秒$\sqrt{2}$个单位长度，点P到达终点时，P，Q同时停止运动. 当点P不与点A，C重合时，过点P作PN⊥AB于点N，连接PQ，以PN，PQ为邻边作□PQMN. 设□PQMN与△ABC重叠部分图形的面积为S，点P的运动时间为t秒.
(1)①AB的长为______；
②PN的长用含t的代数式表示为______.
(2)用代数式表示S.

答案：
5.
(1)①8　②t
(2)如图
(1),当▱PQMN为矩形时，∠NPQ=90°,
　　　　　　　
　由题意可知AP=CQ=$\sqrt{2}$t,CP=BQ=4$\sqrt{2}$−$\sqrt{2}$t.
∵AC=BC,
∴∠A=∠B=45°
∴PN=AN=t.
∵□PQMN为矩形，
∴PN⊥AB,QM⊥AB,QM=PN,此时QM=BM=4−t,
∴4−t=t,
∴t=2,
即当▱PQMN为矩形时,t=2,此时S=8.
　如图
(2)，当0＜t＜2时，▱PQMN在三角形内部，延长QM交AB于点G.
　由题意可知PN=AN=t,BG=QG=4−t,
∴NG=8−AN−BG=8−t−(4−t)=4,
∴▱PQMN与△ABC重叠部分图形的面积S=S▱PQMN=PN·NG=4t;
　　 如图
(3),当2＜t＜4时,▱PQMN与△ABC重叠部分图形为梯形PQGN，
　由题意可知PN=AN=t,BG=QG=4−t,
∴NG=8−AN−BG=8−t−(4−t)=4,
∴▱PQMN与△ABC重叠部分图形的面积S=S梯形PQGN=$\frac{1}{2}$(QG+PN)·NG=$\frac{1}{2}$(4−t+t)×4=8.
　综上所述,S=$\begin{cases}4t(0＜t＜2) \\ 8(2\leq t＜4) \end{cases}$.