《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1. 跨学科 耗能 (2023·深圳中考)爬坡时坡面与水平面夹角为α，则每爬1 m耗能(1.025 - cosα)J，若某人爬了1 000 m，该坡角为30°，则他耗能( ).(参考数据：$\sqrt{3}\approx1.732$，$\sqrt{2}\approx1.414$)
A. 58 J
B. 159 J
C. 1 025 J
D. 1 732 J

答案： B [解析]由题意，得耗能 = 1000×(1.025 - cos30°)=1000×(1.025 - $\frac{\sqrt{3}}{2}$)≈159(J). 故选B.

2. 教材P20随堂练习T2·变式 (2024·眉山中考)如图，斜坡CD的坡度i = 1：2，在斜坡上有一棵垂直于水平面的大树AB，当太阳光与水平面的夹角为60°时，大树在斜坡上的影子BE长为10米，则大树AB的高为______米.
　

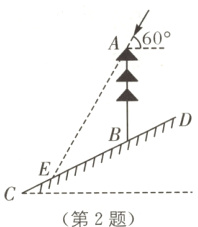
答案：
(4$\sqrt{15}$ - 2$\sqrt{5}$) [解析]如图，过点E作水平地面的平行线，交AB的延长线于点H，则∠BEH = ∠DCF.
在Rt△BEH中，tan∠BEH = tan∠BCF = $\frac{BH}{EH}$ = $\frac{1}{2}$.
设BH = x米，则EH = 2x米，
∴BE = $\sqrt{EH^{2}+BH^{2}}$ = $\sqrt{5}$x = 10，
∴x = 2$\sqrt{5}$，

∴BH = 2$\sqrt{5}$米，EH = 4$\sqrt{5}$米.
∵∠EAH = 180° - 60° - 90° = 30°，
∴AH = $\sqrt{3}$EH = 4$\sqrt{15}$米，
∴AB = AH - BH = (4$\sqrt{15}$ - 2$\sqrt{5}$)米，
故大树AB的高度为(4$\sqrt{15}$ - 2$\sqrt{5}$)米.

3. (2023·赤峰中考)为发展城乡经济，建设美丽乡村，某乡对A地和B地之间的一处垃圾填埋场进行改造，把原来A地去往B地需要绕行到C地的路线，改造成可以直线通行的公路AB.如图，经勘测，AC = 6千米，∠CAB = 60°，∠CBA = 37°，则改造后公路AB的长是______千米.(精确到0.1千米，参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75，$\sqrt{3}\approx1.73$)
　

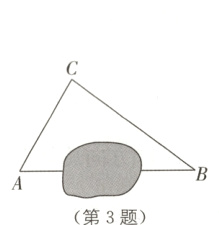
答案： 9.9 [解析]过点C作CD⊥AB于点D.
在Rt△ADC中，AC = 6，∠CAB = 60°，cos∠CAB = $\frac{AD}{AC}$，sin∠CAB = $\frac{CD}{AC}$，
∴AD = AC·cos∠CAB = 6cos60° = 3(千米)，CD = AC·sin∠CAB = 6sin60° = 3$\sqrt{3}$(千米).
在Rt△CDB中，∠CBD = 37°，tan∠CBD = $\frac{CD}{DB}$，
∴DB = $\frac{CD}{tan∠CBD}$ = $\frac{3\sqrt{3}}{tan37°}$≈$\frac{3\sqrt{3}}{0.75}$ = 4$\sqrt{3}$(千米)，
∴AB = AD + DB = 3 + 4$\sqrt{3}$≈3 + 4×1.73≈9.9(千米).
故改造后公路AB的长是9.9千米.

4. 教材P21习题T2·改编 某消防小组在地面A处借助无人机航拍大楼CD.如图，无人机从B处水平飞行至楼顶C处用了12秒，在B，C处测得地面上一点A的俯角分别为75°和30°.已知无人机的飞行速度为5米/秒，求大楼CD的高度.(结果保留根号)
　

答案： 过点B作BE⊥AC于点E，由题意，得CD⊥AD，BC//AD，∠ABM = 75°，∠ACM = 30°，
∴∠BAC = 45°，∠CAD = 30°.
∵BC = 12×5 = 60(米)，
∴AE = BE = 30(米)，
∴CE = BC·cos30° = 30$\sqrt{3}$(米)，
∴AC = AE + CE = (30 + 30$\sqrt{3}$)米，
∴CD = AC·sin30° = (15 + 15$\sqrt{3}$)米.

5. 教材P26复习题T17·改编 (2024·吉林中考)图(1)中的吉林省广播电视塔，又称“吉塔”.某直升飞机于空中A处探测到吉塔，此时飞行高度AB = 873 m，如图(2).从直升飞机上看塔尖C的俯角∠EAC = 37°，看塔底D的俯角∠EAD = 45°，求吉塔的高度CD.(结果精确到0.1 m)(参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)
　　　　　　

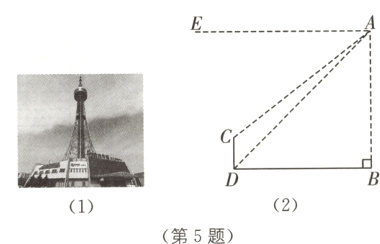
答案：
如图，过点C作CF⊥AB，垂足为F.

由题意，得AE//BD，
∴∠ADB = ∠EAD = 45°，
∴BD = AB = 873 m.
∵AB⊥BD，CF⊥AB，DC⊥BD，
∴∠CDB = ∠B = ∠CFB = 90°，
∴四边形CDBF是矩形，
∴BF = CD，CF = BD = 873 m.
∵CF//BD//AE，
∴∠ACF = ∠EAC = 37°.
在Rt△ACF中，
∵tan∠ACF = $\frac{AF}{CF}$，
∴AF = CF·tan∠ACF = 873×tan37°≈873×0.75 = 654.75(m)，
∴CD = FB = AB - AF = 873 - 654.75≈218.3(m).
故吉塔的高度CD约为218.3 m.