《2025年1课3练江苏人民出版社九年级数学下册北师大版》

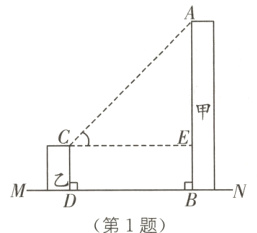
1 教材P26复习题T17·改编 如图，线段AB，CD分别表示甲、乙两栋楼的高，AB⊥MN于点B，CD⊥MN于点D，两座建筑物间的距离BD为40 m.若CD为16 m，在点C处测得点A的仰角∠ACE为45°，则甲建筑物的高AB为______m.

答案： 56 [解析]由题意，得$BE = CD = 16\ m$，$EC = BD = 40\ m$，$AE\perp CE$，在$Rt\triangle ACE$中，$\angle ACE = 45^{\circ}$，$\therefore AE = EC\cdot\tan45^{\circ}= 40\ m$.$\therefore AB = AE + EB = 40 + 16 = 56(m)$.故甲建筑物的高$AB$为$56\ m$.

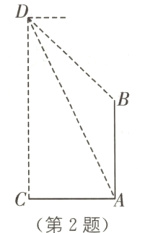
2 (2024·赤峰中考)综合实践课上，航模小组用无人机测量古树AB的高度.如图，点C处与古树底部A处在同一水平面上，且AC = 10米，无人机从C处竖直上升到达D处，测得古树顶部B的俯角为45°，古树底部A的俯角为65°，则古树AB的高度约为______米.(结果精确到0.1米.参考数据：sin 65°≈0.906，cos 65°≈0.423，tan 65°≈2.145)

答案：
11.5 [解析]如图，由题意，知$DM// AC$，$DC\perp AC$，$\angle MDA = 65^{\circ}$，$\angle MDB = 45^{\circ}$.过点$B$作$BE\perp DC$，垂足为$E$.$\because BE\perp CD$，$AB\perp AC$，$DC\perp AC$，$\therefore\angle C=\angle BEC=\angle CAB = 90^{\circ}$.$\therefore$四边形$CABE$是矩形.

$\therefore BE = AC = 10$米，$CE = AB$.$\because DM// AC// BE$，$\therefore\angle MDB=\angle EBD = 45^{\circ}$，$\angle MDA=\angle DAC = 65^{\circ}$.在$Rt\triangle ACD$中，$\because\tan\angle DAC=\frac{DC}{AC}$，$\therefore DC=\tan\angle DAC\cdot AC=\tan65^{\circ}\times10\approx2.145\times10 = 21.45$(米).在$Rt\triangle DBE$中，$\because\tan\angle DBE=\frac{DE}{BE}$，$\therefore DE=\tan\angle DBE\cdot BE=\tan45^{\circ}\times10 = 1\times10 = 10$(米).$\therefore AB = CE = DC - DE = 21.45 - 10 = 11.45\approx11.5$(米).

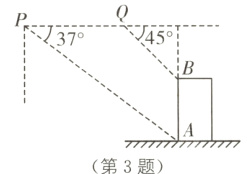
3 教材P25复习题T10·变式 (2024·盐城中考)如图，小明用无人机测量教学楼的高度，将无人机垂直上升距地面30 m的点P处，测得教学楼底端点A的俯角为37°，再将无人机沿教学楼方向水平飞行26.6 m至点Q处，测得教学楼顶端点B的俯角为45°，则教学楼AB的高度约为______m.(结果精确到1 m，参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)

答案：
17 [解析]如图，设$AB$的延长线与$PQ$的延长线交于点$C$.

由题意，知$AC = 30\ m$，$PQ = 26.6\ m$，$\angle APC = 37^{\circ}$，$\angle BQC = 45^{\circ}$，在$Rt\triangle APC$中，$PC=\frac{AC}{\tan37^{\circ}}\approx\frac{30}{0.75}= 40(m)$，$\therefore QC = PC - PQ = 40 - 26.6 = 13.4(m)$.在$Rt\triangle BQC$中，$BC = QC = 13.4\ m$，$\therefore AB = AC - BC = 30 - 13.4 = 16.6\approx17(m)$.

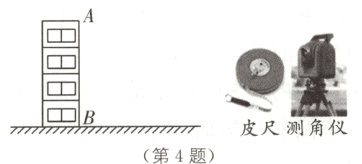
4 (2024·包头中考)如图，学校数学兴趣小组开展“实地测量教学楼AB的高度”的实践活动.教学楼周围是开阔平整的地面，可供使用的测量工具有皮尺、测角仪(皮尺的功能是直接测量任意可到达的两点间的距离；测角仪的功能是测量角的大小).
(1)请你设计测量教学楼AB的高度的方案，方案包括画出测量平面图，把应测数据标记在所画的图形上(测出的距离用m，n等表示，测出的角用α，β等表示)，并对设计进行说明；
(2)根据你测量的数据，计算教学楼AB的高度.(用字母表示)

答案：

(1)如图，在地面上取$C$，测量$BC = m$，测量$\angle ACB=\alpha$，根据$\tan\alpha=\frac{AB}{BC}$，即可得出$AB$的长度.

(2)$\because\angle ABC = 90^{\circ}$，$\therefore\tan\alpha=\frac{AB}{BC}$，$\therefore AB = BC\times\tan\alpha=m\tan\alpha$.

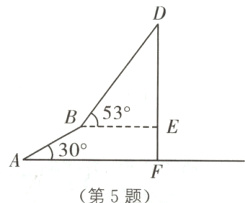
5 (2023·本溪中考)暑假期间，小明与小亮相约到某旅游风景区登山.需要登顶600 m高的山峰，由山底A处先步行300 m到达B处，再由B处乘坐登山缆车到达山顶D处.已知点A，B，D，E，F在同一平面内，山坡AB的坡角为30°，缆车行驶路线BD与水平面的夹角为53°.(换乘登山缆车的时间忽略不计)
(1)求登山缆车上升的高度DE；
(2)若步行速度为30 m/min，登山缆车的速度为60 m/min，求从山底A处到达山顶D处大约需要多少分钟.(结果精确到0.1 min，参考数据：sin 53°≈0.80，cos 53°≈0.60，tan 53°≈1.33)

答案：
(1)过点$B$作$BM\perp AF$于点$M$，由题意可知，$\angle A = 30^{\circ}$，$\angle DBE = 53^{\circ}$，$DF = 600\ m$，$AB = 300\ m$，在$Rt\triangle ABM$中，$\angle A = 30^{\circ}$，$AB = 300\ m$，$\therefore BM=\frac{1}{2}AB = 150\ m = EF$，$\therefore DE = DF - EF = 600 - 150 = 450(m)$.故登山缆车上升的高度$DE$为$450\ m$.
(2)在$Rt\triangle BDE$中，$\angle DBE = 53^{\circ}$，$DE = 450\ m$，$\therefore BD=\frac{DE}{\sin\angle DBE}\approx\frac{450}{0.80}= 562.5(m)$，$\therefore$需要的时间$t = t_{步行}+t_{缆车}=\frac{300}{30}+\frac{562.5}{60}\approx19.4(min)$.故从山底$A$处到达山顶$D$处大约需要$19.4\ min$.