《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

18.[答案含评分细则](2024河南中考)(6分)如图，矩形ABCD的四个顶点都在格点(网格线的交点)上，对角线AC，BD相交于点E，反比例函数y = k/x(x ＞ 0)的图象经过点A.
(1)求这个反比例函数的表达式.
(2)请先描出这个反比例函数图象上不同于点A的三个格点，再画出反比例函数的图象.
(3)将矩形ABCD向左平移，当点E落在这个反比例函数的图象上时，平移的距离为_______.
　　　　　　　　

答案：
解析　
(1)
∵ 反比例函数y = k/x(x＞0)的图象经过点A(3,2)，
∴ 2 = k/3，
∴ k = 6，
　
∴ 这个反比例函数的表达式为y = 6/x.　　　　　2分
(2)如图.
　　　　　
　　　　　　　　　　　　　　　　　　　4分
(3)9/2　　　　　　　　　　　　　　　　　　6分

19.[答案含评分细则](6分)如图，AB是公园的一圆形桌面的主视图，MN表示该桌面在路灯下的影子，CD表示一个圆形的凳子面的主视图.
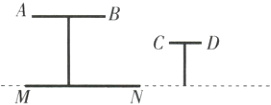
(1)请你在图中标出路灯O的位置，并画出CD的影子PQ(要求保留画图痕迹，光线用虚线表示)；
(2)若桌面直径和桌面与地面的距离均为1.2 m，测得影子的最大跨度MN为2 m，求路灯O与地面的距离.
　　　　　　　　

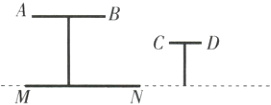
答案：
解析　
(1)如图，分别连接MA、NB并延长，它们的交点为点O，即点O为路灯的位置，连接OC、OD，并延长分别交地面于点P、Q，则PQ为CD的影子，所以点O和PQ即为所求.
　　　　　
　　　　　　　　　　　　　　　　　　　3分
(2)过点O作OF⊥MN于点F，OF交AB于点E，如图，由题可知AB = 1.2m，EF = 1.2m，MN = 2m，
∵ AB//MN，
∴ △OAB∽△OMN，
∴ AB:MN = OE:OF，即1.2:2 = (OF - 1.2):OF，
∴ OF = 3m.
　答:路灯O与地面的距离为3m.　　　　　　　6分

20.[答案含评分细则](2024黑龙江龙东地区中考)(7分)为了增强学生的体质，某学校倡导学生在大课间开展踢毽子活动，需购买甲、乙两种品牌毽子，已知购买甲种品牌毽子10个和乙种品牌毽子5个共需200元；购买甲种品牌毽子15个和乙种品牌毽子10个共需325元.
(1)购买一个甲种品牌毽子和一个乙种品牌毽子各需要多少元？
(2)若购买甲、乙两种品牌毽子共花费1 000元，甲种品牌毽子数量不低于乙种品牌毽子数量的5倍且不超过乙种品牌毽子数量的16倍，则有哪几种购买方案？
(3)若商家每售出一个甲种品牌毽子的利润是5元，每售出一个乙种品牌毽子的利润是4元，在(2)的条件下，学校如何购买毽子商家获得的利润最大？最大利润是多少元？

答案： 解析　
(1)设购买一个甲种品牌毽子需要x元，一个乙种品牌毽子需要y元，
　根据题意得{10x + 5y = 200, 15x + 10y = 325}，解得{x = 15, y = 10}.
　答:购买一个甲种品牌毽子需要15元，一个乙种品牌毽子需要10元.　　　　　　　　　　　　　2分
(2)设购买m个甲种品牌毽子，则购买(1000 - 15m)/10 = (100 - 3/2m)个乙种品牌毽子，
　根据题意得{m≥5(100 - 3/2m), m≤16(100 - 3/2m)}，
　解得1000/17≤m≤64，
　又
∵ m，100 - 3/2m均为正整数，
∴ m可以为60，62，64，
∴ 学校共有3种购买方案:
　方案1:购买60个甲种品牌毽子，10个乙种品牌毽子;
　方案2:购买62个甲种品牌毽子，7个乙种品牌毽子;
　　方案3:购买64个甲种品牌毽子，4个乙种品牌毽子.
　　　　　　　　　　　　　　　　　　　4分
(3)学校选择方案1，商家可获得的利润为5×60 + 4×10 = 340(元);
　　学校选择方案2，商家可获得的利润为5×62 + 4×7 = 338(元);
　　学校选择方案3，商家可获得的利润为5×64 + 4×4 = 336(元).
　
∵ 340 ＞ 338 ＞ 336，
　
∴ 在
(2)的条件下，学校购买60个甲种品牌毽子，10个乙种品牌毽子时，商家获得的利润最大，最大利润是340元.　　　　　　　　　　　　　　　　　7分