《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

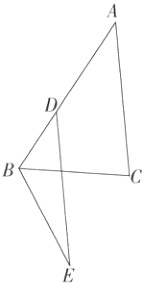
20. [答案含评分细则](8分)如图，在△ABC中，∠ABC = 60°，将AC沿AB的方向平移，平移距离为BC的长，得到线段DE，连接BE.
(1)求∠CBE的度数；
(2)在BC上取一点F，且BF = BD，连接AF，DF，求证：AF = DE.

答案：
解析
(1)连接CE，如图，
　　　　　　　　
∵将AC沿AB的方向平移，平移距离为BC的长，得到线段DE，
∴AD = BC，四边形ADEC为平行四边形，
∴AD = CE，AD//CE， ……………………… 2分
∴∠BCE = ∠ABC = 60°，BC = CE，
∴△BCE为等边三角形，
∴∠CBE = 60°.
……………………………………………… 4分
(2)证明：如图，
∵∠DBF = 60°，BD = BF，
∴△BDF为等边三角形，
∴DF = BD，∠BDF = 60°，
∴∠ADF = 180° - ∠BDF = 120°，又
∵∠EBD = ∠CBE + ∠DBF = 120°，
∴∠ADF = ∠EBD，
∵△BCE为等边三角形，
∴BE = BC，
∴BE = AD. ……………………… 6分
在△ADF和△EBD中，{AD = EB, ∠ADF = ∠EBD, DF = BD}，
∴△ADF≌△EBD(SAS)，
∴AF = DE. ……………………………………… 8分

21. [答案含评分细则](2024北京大兴二模)(8分)在数学活动课上，同学们分组测量学校旗杆的高度，经过交流、研讨及测量给出如下两种方案，请你选择一种方案求出旗杆的高度.
　

答案： 解析 方案一：由题意得∠DEF = ∠ABC = 90°，DF//AC，
∴∠DFE = ∠ACB，
∴△DEF∽△ABC，
∴DE/AB = EF/BC，
∵DE = 1.8米，EF = 0.9米，BC = 6米，
∴1.8/AB = 0.9/6，
∴AB = 12米.答：旗杆的高度为12米. ……………………… 8分
方案二：由题意得∠DEC = ∠ABC = 90°，∠DCE = ∠ACB，
∴△DEC∽△ABC，
∴DE/AB = EC/BC，
∵DE = 1.6米，EC = 1.2米，BC = 9米，
∴1.6/AB = 1.2/9，
∴AB = 12米.答：旗杆的高度为12米. ……………………… 8分

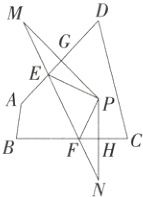
22. [答案含评分细则](2024福建泉州晋江期末)(8分)如图，点P在四边形ABCD的内部，且点P与点M关于AD对称，PM交AD于点G，点P与点N关于BC对称，PN交BC于点H，MN分别交AD，BC于点E，F.
(1)连接PE，PF，若MN = 12 cm，求△PEF的周长；
(2)若∠C + ∠D = 134°，求∠HPG的度数.
　　　　　　　　　　　　　

答案： 解析
(1)
∵点P与点M关于AD对称，点P与点N关于BC对称，
∴EM = EP，FP = FN，
∴C△PEF = PE + PF + EF = ME + EF + FN = MN = 12 cm.…
……………………………………………… 3分
(2)
∵∠C + ∠D = 134°，
∴∠A + ∠B = 360° - 134° = 226°， ………………… 5分
又
∵PG⊥AD，PH⊥BC，
∴∠PGA = ∠PHB = 90°，
∴∠HPG = 540° - 90° - 90° - 226° = 134°. ……… 8分