《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

14.(2024北京八十中月考,21,★☆☆)某种产品的形状是长方体,长为8 cm,它的展开图如图所示.
(1)求长方体的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装8件这种产品,要求设计时不计空隙且该纸箱所用材料最少(纸箱的表面积最小),并求出你设计的纸箱的表面积.

答案： 解析　
(1)设长方体的高为xcm,则长方体的宽为(12−2x)cm,
　　根据题意可得12−2x + 8 + x + 8 = 25,解得x = 3,
　　所以长方体的高为3cm,宽为6cm,所以长方体的体积为8×6×3 = 144($cm^{3}$).
(2)因为长方体的高为3cm,宽为6cm,长为8cm,所以装8件这种产品，应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少，这样的话,4件这种产品可以用12×6×8的包装纸箱，再考虑12×8 的面积最大,所以12×8的面重叠在一起,这时纸箱所用材料最少,所以设计的包装纸箱为12×12×8规格,该产品的侧面积分别为2×8×12 = 192($cm^{2}$),12×12 = 144($cm^{2}$),
　　纸箱的表面积为(192 + 144)×2 = 672($cm^{2}$).
　　答:纸箱的表面积为672 $cm^{2}$.

15.[空间观念]如图,在长方体ABCD - A'B'C'D'中,点E是棱B'C'的中点,已知AB = 3 cm,BC = 4 cm,AA' = 5 cm.一只小虫从A点出发沿长方体的表面到E点处觅食,求小虫爬行的最短距离.

答案：
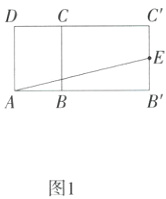
解析　将面B'C'CB沿BC展开,平面图为图1,
∴AE = $\sqrt{(5 + 3)^{2}+2^{2}}=\sqrt{68}=2\sqrt{17}$ cm.
　　将面A'B'C'D'沿A'B'展开,平面图为图2,
∴AE = $\sqrt{3^{2}+(5 + 2)^{2}}=\sqrt{58}$ cm.
　　将面B'BCC'沿BB'展开,平面图为图3,
∴AE = $\sqrt{(3 + 2)^{2}+5^{2}}=\sqrt{50}=5\sqrt{2}$ cm.
　　因为$5\sqrt{2}＜\sqrt{58}＜2\sqrt{17}$,所以小虫爬行的最短距离为$5\sqrt{2}$ cm.
　 　　

1.(2024四川达州中考)如图,正方体的表面展开图上写有“我们热爱中国”六个字,还原成正方体后,“我”的对面上的字是 （ ）

A.热
B.爱
C.中
D.国

答案： 1B　根据在同一行的，隔一个便是相对面得“热”与“国”相对.根据“Z”型两端即为相对面得“我”与“爱”相对，“们”与“中”相对.故选B.

2.(2024河北保定高碑店三模)用硬卡纸做一个骰子,使骰子相对面上的两个点数之和为7,折叠前后如图所示,下列判断正确的是 （ ）

A.点数1的对面是B面
B.点数2的对面是A面
C.A,C两个面的点数和为9
D.B,C两个面的点数和为6

答案： 2C由题意得点数1和A面是相对面，点数2和B面是相对面，点数4和C面是相对面，
∵相对面上的两个点数之和为7,
∴A面的点数是6,B面的点数是5,C面的点数是3,
∴A,C两个面的点数和为9,B,C 两个面的点数和为8,故选C.