《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

1.(2023北京海淀二模)如图,在正方形网格中,以点O为位似中心,△ABC的位似图形可以是(M9223006) ( )

A.△DEF
B.△DHF
C.△GEH
D.△GDH

答案：
C如图,
∵△ABC与△GEH是相似图形，而且对应顶点的连线相交于点O，对应边互相平行，
∴△ABC与△GEH是位似图形,故选C.

2.[北京名胜古迹·紫禁城](2024北京北大附中零模)2020年是紫禁城建成600年暨故宫博物院成立95周年,在此之前有多个国家曾发行过紫禁城元素的邮品.图1是摩纳哥发行的小型张中的图案,以敞开的紫禁城大门、大门内的石狮和太和殿作为邮票和小型张的边饰,如果标记出图1中大门的门框并画出相关的几何图形(图2),我们发现设计师巧妙地使用了数学元素(忽略误差),图2中的四边形ABCD与四边形A'B'C'D'是位似图形,点O是位似中心,点A'是线段OA的中点,那么以下结论正确的是( )

A.四边形ABCD与四边形A'B'C'D'的相似比为1∶1
B.四边形ABCD与四边形A'B'C'D'的相似比为1∶2
C.四边形ABCD与四边形A'B'C'D'的周长比为3∶1
D.四边形ABCD与四边形A'B'C'D'的面积比为4∶1

答案： D
∵点A'是线段OA的中点，
∴OA:OA'=2:1,
∵四边形ABCD与四边形A'B'C'D'是位似图形，点O是位似中心，
∴AB:A'B'=2:1,
∴四边形ABCD 与四边形A'B'C'D'的相似比为2:1,周长比为2:1,面积比为4:1.故选D.

3.如图,以点O为位似中心,在点O的同侧画一个四边形A'B'C'D',使它与四边形ABCD位似,且相似比为3∶2,则下列说法错误的是( )

A.四边形ABCD∽四边形A'B'C'D'
B.C,O,C'三点在同一条直线上
C.$\frac{AB}{A'B'}=\frac{2}{3}$
D.$OB=\frac{3}{5}OB'$

答案： D
∵四边形A'B'C'D'与四边形ABCD位似，
∴四边形A'B'C'D'∽四边形ABCD，C，O，C'三点在同一条直线上，
∴A、B选项说法正确;
　
∵四边形A'B'C'D'与四边形ABCD位似,相似比为3:2,
∴AB//A'B'，$\frac{AB}{A'B'}=\frac{2}{3}$，
　
∴△OAB∽△OA'B'，
　
∴$\frac{OB}{OB'}=\frac{AB}{A'B'}=\frac{2}{3}$（C选项说法正确），
∴OB = $\frac{2}{3}$OB'，
∴D选项说法错误.故选D.

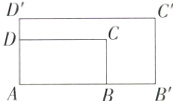
4.如图,已知矩形ABCD与矩形AB'C'D'是位似图形,A为位似中心,且矩形ABCD的周长为24,BB'=4,DD'=2.求AB、AD的长.(M9223006)

答案： 解析
∵矩形ABCD的周长为24，
∴AB+AD=12.
　　设AB=x，则AB'=AB+BB'=x+4，AD=12−x.
　
∴AD'=AD+DD'=14−x.
　
∵矩形ABCD与矩形AB'C'D'是位似图形，
∴$\frac{AB}{AB'}=\frac{AD}{AD'}$，即$\frac{x}{x+4}=\frac{12−x}{14−x}$，解得x=8，经检验，x=8 是分式方程的解，
　
∴AB=8，
∴AD=4.

5.[教材变式·P25例1]如图,点O是△ABC外一点.(M9223006)
(1)以O为位似中心,将△ABC各边放大为原来的2倍;(不写作法,保留作图痕迹)
(2)满足(1)中条件的三角形共有几个?它们是不是位似图形?

答案：
解析　
(1)如图所示,△A'B'C'和△A''B''C''即为所求作的三角形.
　　
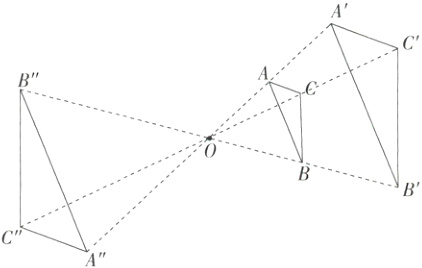
(2)满足
(1)中条件的三角形有两个，它们是位似图形.