《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

1.(2024四川凉山州中考)点P(a,−3)关于原点对称的点是P'(2,b)，则a+b的值是　　　(　　　)
A.1　　　
　B.−1　　
　C.−5　　
　D.5

答案： 1A
∵点P(a,−3)关于原点对称的点是P'(2,b),
∴a=−2,b=3,
∴a+b=1,故选A.

2.如图,直线y = - $\frac{4}{3}$x + 4与x轴、y轴分别交于A、B两点,
　　　　　　　　　　　　
△AOB绕点A顺时针旋转90°后得到△AO'B'，则点B的对应点B'的坐标为　　　　　　　　　　(　　　)
A.(3,4)　　　　　　
　B.(7,4)
C.(7,3)　　　　　　
　D.(3,7)

答案： 2C 当x=0时,y=−$\frac{4}{3}$x + 4 = 4,则B点的坐标为(0,4),则OB=4;当y=0时,−$\frac{4}{3}$x + 4 = 0,解得x=3,则A点的坐标为(3,0),则OA=3.
∵△AOB绕点A顺时针旋转90°后得到△AO'B',
∴∠OAO'=90°,∠AO'B'=∠AOB=90°,AO'=AO=3,O'B'=OB=4,即AO'⊥x轴,O'B'//x轴,
∴点B'的坐标为(7,3).故选C.

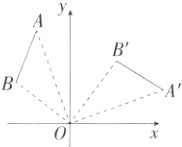
3.如图,将线段AB绕点O顺时针旋转90°得到线段A'B',那么A(−1,4)的对应点A'的坐标是________.(M9223003)
　　　　　　

答案：
答案　(4,1)
解析
∵线段AB绕点O顺时针旋转90°得到线段A'B',
∴△ABO≌△A'B'O,∠AOA'=90°,
∴AO=A'O.如图,作AC⊥y轴于C,A'C'⊥x轴于C',
∴∠ACO=∠A'C'O=90°.
∵∠COC'=90°,
∴∠AOA'−∠COA'=∠COC'−∠COA',
∴∠AOC=∠A'OC'.
在△ACO和△A'C'O中,
$\begin{cases}∠ACO = ∠A'C'O,\\∠AOC = ∠A'OC',\\AO = A'O\end{cases}$
∴△ACO≌△A'C'O(AAS),
∴AC=A'C',CO=C'O.
∵A(−1,4),
∴AC=1,CO=4,
∴A'C'=1,OC'=4,
∴A'(4,1).

4.(2024北京陈经纶中学帝景分校月考)如图,在平面直角坐标系中,△ABC的各顶点都在格点上,点A,B,C的坐标分别为(−1,2),(−3,1),(0,−1),将△ABC绕点C按顺时针方向旋转90°,画出旋转后的△A1B1C,并写出此时点A,点B 的对应点A1,B1的坐标.(M9223003)
　　　　　　　　　

答案：
解析　如图所示，△A₁B₁C即为所求.

由图可知A₁(3,0),B₁(2,2).

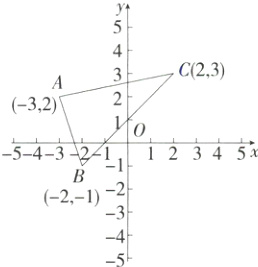
5.教材变式·P14例3 如图,画出△ABC关于原点O对称的△A1B1C1,并写出点A1、B1、C1的坐标.
　　　

答案：
解析　如图所示，△A₁B₁C₁即为所求作的三角形，A₁(3,−2),B₁(2,1),C₁(−2,−3).

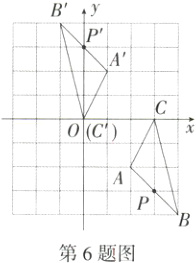
6.(2024山东青岛一模改编,8,★☆☆)如图,把图中的△ABC经过一定的变换得到△A'B'C',如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P'的坐标为　　　　　　　　　(　　　)
[中点坐标公式:若点A(x1,y1)，点B(x2,y2)，则线段AB的中点坐标为($\frac{x_1 + x_2}{2}$,$\frac{y_1 + y_2}{2}$)]
A.(a - 3,b)　　　　　　B.(a + 3,b)
C.(3 - a,-b)　　　　　D.(a - 3,-b)
　　　　

答案： 6C 由题图可知△ABC与△A'B'C'关于点(1.5,0)成中心对称,设点P'的坐标为(x,y),所以$\frac{a + x}{2}$=1.5,$\frac{b + y}{2}$=0,解得x=3 - a,y=-b,所以P'(3 - a,-b).故选C.

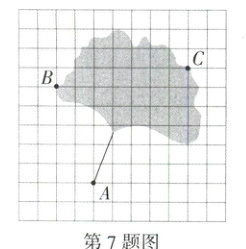
7.跨生物·标本(2023山东枣庄中考,13,★☆☆)银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如图所示的是一片银杏叶标本,叶片上两点B,C的坐标分别为(−3,2),(4,3),将银杏叶绕原点顺时针旋转90°后,叶柄上点A的对应点的坐标为________.(M9223003)

答案：
答案　(−3,1)
解析　如图,建立平面直角坐标系,则点A的坐标为(−1,−3),作出点A绕原点O顺时针旋转90°得到的对应点A',则点A'的坐标为(−3,1).