《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

9.应用意识 情境·中华优秀传统文化（2023湖北十堰中考）“端午节”吃粽子是中国传统习俗，在“端午节”来临前，某超市购进一种品牌的粽子，每盒进价是40元，并规定每盒售价不得少于50元，日销售量不低于350盒.根据以往销售经验发现，当每盒售价定为50元时，日销售量为500盒，每盒售价每提高1元，日销售量减少10盒.设每盒售价为x元，日销售量为p盒.
（1）当x = 60时，p = _______.
（2）当每盒售价定为多少元时，日销售利润W（元）最大？最大利润是多少？
（3）小强说：“当日销售利润最大时，日销售额不是最大.”小红说：“当日销售利润不低于8000元时，每盒售价x的范围为60≤x≤80.”你认为他们的说法正确吗？若正确，请说明理由；若不正确，请写出正确的结论.

答案： 解析 （1）由题意可得，p = 500 - 10(x - 50) = -10x + 1000，即日销售量p（盒）与每盒售价x（元）之间的函数关系式是p = -10x + 1000(x≥50)，当x = 60时，p = -10×60 + 1000 = 400.
（2）由题意，得W = (x - 40)(-10x + 1000) = -10x² + 1400x - 40000 = -10(x - 70)² + 9000，
由题可知，每盒售价不得少于50元，日销售量不低于350盒，
∴$\begin{cases}x≥50 \\ p≥350\end{cases}$，即$\begin{cases}x≥50 \\ -10x + 1000≥350\end{cases}$，解得50≤x≤65.
又
∵ -10＜0，对称轴为直线x = 70，
∴当x = 65时，W取得最大值，此时W = 8750.
答：当每盒售价定为65元时，日销售利润W（元）最大，最大利润是8750元.
（3）小强：设日销售额为y元，则y = x·p = x(-10x + 1000) = -10x² + 1000x = -10(x - 50)² + 25000，
∵50≤x≤65，
∴当x = 50时，y值最大，此时y = 25000，而当x = 65时，W值最大，此时W = 8750，
∴小强的说法正确.
小红：当 -10(x - 70)² + 9000 = 8000时，解得x = 60或x = 80，
∵ -10＜0，
∴当日销售利润不低于8000元时，60≤x≤80，
又
∵50≤x≤65，
∴当日销售利润不低于8000元时，60≤x≤65，故小红的说法错误，正确的结论是当日销售利润不低于8000元时，60≤x≤65.

例 如图所示，校园前门花园上有一面墙，长度为12m，地铁施工，需要隔离部分矩形地块，用长为26m的篱笆和这面墙围成了80m²的矩形，则AB和BC的长分别为_________.

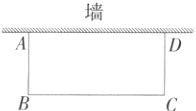
答案： 答案 8 m，10 m
解析 设AB的长为x米，则BC的长为(26 - 2x)米，
根据题意，得x(26 - 2x) = 80，解得x₁ = 8，x₂ = 5. 当x = 5时，26 - 2x = 26 - 2×5 = 16＞12（不合题意，舍去）；当x = 8时，26 - 2x = 26 - 2×8 = 10. 故AB = 8 m，BC = 10 m.

变式【无门→单门→双门】
1.某驻村工作队为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下围一块面积为600m²的矩形实验茶园，便于成功后大面积推广.如图所示，茶园一面靠墙，墙长35m，另外三面用69m长的篱笆围成，其中一边开有一扇1m宽的门（不包括篱笆），则AB的长为________.

答案： 答案 20 m
解析 设AB的长为x m，则BC的长为(69 + 1 - 2x)m，
依题意得x(69 + 1 - 2x) = 600，整理得x² - 35x + 300 = 0，解得x₁ = 15，x₂ = 20，
当x = 15时，
69 + 1 - 2x = 69 + 1 - 2×15 = 40＞35，不符合题意，舍去；
当x = 20时，
69 + 1 - 2x = 69 + 1 - 2×20 = 30＜35，符合题意.
∴AB的长为20 m.

2.如图，有长为22m的篱笆，一面利用墙（墙的最大可用长度为14m），围成中间隔有一道篱笆的矩形花圃ABCD，为了方便出入，在建造篱笆花圃时，在BC上用其他材料造了两个宽为1m的小门.若花圃的面积刚好为45m²，则AB的长为________.

答案： 答案 5 m
解析 设AB的长为x m，则BC的长为(22 + 2 - 3x)m，
依题意得x(22 + 2 - 3x) = 45，
整理得x² - 8x + 15 = 0，解得x₁ = 3，x₂ = 5，
当x = 3时，
22 + 2 - 3x = 22 + 2 - 3×3 = 15＞14，不符合题意，舍去；
当x = 5时，
22 + 2 - 3x = 22 + 2 - 3×5 = 9＜14，符合题意.
∴AB的长为5 m.