第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
21.(10分)综合与实践:制作无盖盒子.
任务一:如图①,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为616cm³的无盖长方体盒子.(纸板厚度忽略不计)
(1)请在如图①所示的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
(2)求出这块矩形纸板的长和宽.
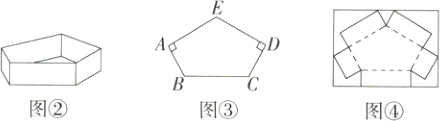
任务二:图②是一个高为4cm的无盖的五棱柱盒子(直棱柱),图③是其底面,在五边形ABCDE中,BC = 12cm,AB = DC = 6cm,∠ABC = ∠BCD = 120°,∠EAB = ∠EDC = 90°.
(3)试判断图③中AE与DE的数量关系,并加以证明.
(4)图②中的五棱柱盒子可按如图④所示的方式将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少? 请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗均忽略不计).

任务一:如图①,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为616cm³的无盖长方体盒子.(纸板厚度忽略不计)
(1)请在如图①所示的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
(2)求出这块矩形纸板的长和宽.
任务二:图②是一个高为4cm的无盖的五棱柱盒子(直棱柱),图③是其底面,在五边形ABCDE中,BC = 12cm,AB = DC = 6cm,∠ABC = ∠BCD = 120°,∠EAB = ∠EDC = 90°.
(3)试判断图③中AE与DE的数量关系,并加以证明.
(4)图②中的五棱柱盒子可按如图④所示的方式将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少? 请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗均忽略不计).


答案:
21解析
(1)按要求画出示意图(如图).

(2)设矩形纸板的宽为xcm,则长为2xcm.
由题意,得4(x - 2×4)(2x - 2×4)= 616,
解得$x_1 = 15$,$x_2 = - 3$(不合题意,舍去),
则2x=2×15=30.
答:矩形纸板的长为30cm,宽为15cm.
(3)AE=DE.证明如下:
如图,延长EA,ED分别交直线BC于点M,N;

∵∠ABC=∠BCD=120°,
∴∠ABM=∠DCN=60°.又
∵∠EAB=∠EDC=90°,
∴∠M=∠N=90°−60°=30°,
∴EM=EN.
在△MAB与△NDC中,$\begin{cases}\angle M=\angle N,\\\angle ABM=\angle DCN,\\AB = DC\end{cases}$
∴△MAB≌△NDC,
∴AM=DN,
∴EM−AM=EN−DN,即AE=DE.
(4)长至少为(18 + 4$\sqrt{3}$)cm,宽至少为(4 + 8$\sqrt{3}$)cm.
21解析
(1)按要求画出示意图(如图).

(2)设矩形纸板的宽为xcm,则长为2xcm.
由题意,得4(x - 2×4)(2x - 2×4)= 616,
解得$x_1 = 15$,$x_2 = - 3$(不合题意,舍去),
则2x=2×15=30.
答:矩形纸板的长为30cm,宽为15cm.
(3)AE=DE.证明如下:
如图,延长EA,ED分别交直线BC于点M,N;

∵∠ABC=∠BCD=120°,
∴∠ABM=∠DCN=60°.又
∵∠EAB=∠EDC=90°,
∴∠M=∠N=90°−60°=30°,
∴EM=EN.
在△MAB与△NDC中,$\begin{cases}\angle M=\angle N,\\\angle ABM=\angle DCN,\\AB = DC\end{cases}$
∴△MAB≌△NDC,
∴AM=DN,
∴EM−AM=EN−DN,即AE=DE.
(4)长至少为(18 + 4$\sqrt{3}$)cm,宽至少为(4 + 8$\sqrt{3}$)cm.
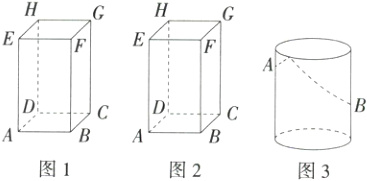
22.(2024安徽芜湖无为月考)(12分)如图1和2,长方体的长(AB)为4cm,宽(BC)为3cm,高为12cm.
(1)如图1,求该长方体中能放入木棒的最大长度.
(2)如图2,现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)如图3,若将题中的长方体换成圆柱形容器(容器厚度忽略不计),容器的高为12cm,底面周长为12cm,在容器内壁离底部5cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿1cm与饭粒相对的点A处.问蚂蚁吃到饭粒需要爬行的最短路程是多少?
(1)如图1,求该长方体中能放入木棒的最大长度.
(2)如图2,现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)如图3,若将题中的长方体换成圆柱形容器(容器厚度忽略不计),容器的高为12cm,底面周长为12cm,在容器内壁离底部5cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿1cm与饭粒相对的点A处.问蚂蚁吃到饭粒需要爬行的最短路程是多少?

答案:
22解析
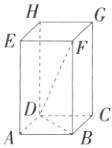
(1)连接DF,如图,该长方体中能放入木棒的最大长度是$\sqrt{(\sqrt{3^2 + 4^2})^2+12^2}=13$ cm.
(2)①如图,将下面与右面展开,连接AG,则AG=$\sqrt{(4 + 12)^2+3^2}=\sqrt{265}$ cm.
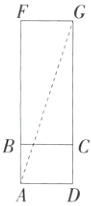
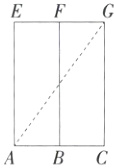
②如图,将前面与上面展开,连接AG,则AG=$\sqrt{(3 + 12)^2+4^2}=\sqrt{241}$ cm.
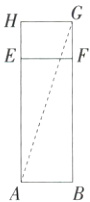
③如图,将前面与右面展开,连接AG,则AG=$\sqrt{(3 + 4)^2+12^2}=\sqrt{193}$ cm.
∵$\sqrt{265}>\sqrt{241}>\sqrt{193}$
∴蚂蚁爬行的最短路程为$\sqrt{193}$ cm.
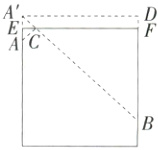
(3)将容器侧面展开,作A关于EF的对称点A',作A'D⊥BF,交BF的延长线于D,
∴A'D=6cm,BD=12−5+1=8cm,
连接A'B,交EF于C,连AC,则A'B的长即为最短路程,
∴A'B=$\sqrt{A'D^2+BD^2}=10$ cm.
.方法解读
本题是立体图形表面上的最短路径问题.“化曲为直”是解决此类问题的关键,先将立体图形转化为平面图形,然后利用“两点之间,线段最短”找到最短路径,再用勾股定理计算.
22解析
(1)连接DF,如图,该长方体中能放入木棒的最大长度是$\sqrt{(\sqrt{3^2 + 4^2})^2+12^2}=13$ cm.

(2)①如图,将下面与右面展开,连接AG,则AG=$\sqrt{(4 + 12)^2+3^2}=\sqrt{265}$ cm.

②如图,将前面与上面展开,连接AG,则AG=$\sqrt{(3 + 12)^2+4^2}=\sqrt{241}$ cm.

③如图,将前面与右面展开,连接AG,则AG=$\sqrt{(3 + 4)^2+12^2}=\sqrt{193}$ cm.

∵$\sqrt{265}>\sqrt{241}>\sqrt{193}$
∴蚂蚁爬行的最短路程为$\sqrt{193}$ cm.
(3)将容器侧面展开,作A关于EF的对称点A',作A'D⊥BF,交BF的延长线于D,
∴A'D=6cm,BD=12−5+1=8cm,
连接A'B,交EF于C,连AC,则A'B的长即为最短路程,
∴A'B=$\sqrt{A'D^2+BD^2}=10$ cm.

.方法解读
本题是立体图形表面上的最短路径问题.“化曲为直”是解决此类问题的关键,先将立体图形转化为平面图形,然后利用“两点之间,线段最短”找到最短路径,再用勾股定理计算.
查看更多完整答案,请扫码查看


