《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

1. [新独家原创]下列现象：①摩托车在急刹车时向前滑动；②幸运大转盘转动的过程；③钟表的指针的转动；④钟摆的运动. 其中属于旋转的有（M9223003） （ ）
A.4个
B.3个
C.2个
D.1个

答案： B 摩托车在急刹车时向前滑动属于平移;幸运大转盘转动、钟表的指针的转动、钟摆的运动都属于旋转，故选B.

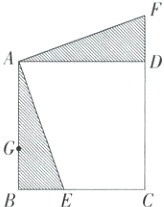
2. [教材变式·P11例1]如图，在正方形ABCD中，E是BC上一点，△ABE经过旋转得到△ADF.（M9223003）
（1）旋转中心是点________；
（2）旋转角最小是________°；
（3）如果点G是AB上的一点，那么经过上述旋转后，点G旋转到什么位置？请在图中将点G的对应点G'表示出来.

答案：
解析
(1)A.
(2)90.
(3)点G旋转到了AD的边上,点G'的位置如图所示.

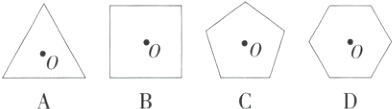
3.（2024北京陈经纶中学一模）以下图形绕点O旋转一定角度后都能与原图形重合，其中旋转角最小的是 （ ）

答案： D 选项A，最小旋转角度=$\frac{360^{\circ}}{3}=120^{\circ}$；选项B，最小旋转角度=$\frac{360^{\circ}}{4}=90^{\circ}$；选项C，最小旋转角度=$\frac{360^{\circ}}{5}=72^{\circ}$；选项D，最小旋转角度=$\frac{360^{\circ}}{6}=60^{\circ}$.故选D.

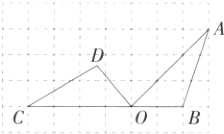
4.（2024北京师大二附中西城实验学校模拟）如图，A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转得到的，则旋转角的度数是 （ ）

A.45°
B.90°
C.120°
D.135°

答案： D
∵△COD是由△AOB绕点O按逆时针方向旋转得到的，
∴旋转角为∠COA，
∵∠COA = 180° - ∠AOB，∠AOB = 45°，
∴旋转角的度数为135°.

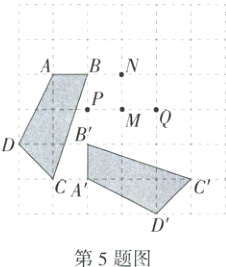
5.（2023北京朝阳期末）在如图所示的正方形网格中，四边形ABCD绕某一点旋转某一角度得到四边形A'B'C'D'（所有顶点都在网格线的交点上），在网格线交点M，N，P，Q中，可能是旋转中心的是（M9223003） （ ）

A.点M
B.点N
C.点P
D.点Q

答案：
A 如图，连接AA'、BB'、CC'，作AA'，BB'，CC'的垂直平分线，交于点M，所以旋转中心是点M.

6. [新独家原创]如图，在△ABO中，∠BAO = 90°，AO = 1，OB = 2，将△ABO绕点O旋转到△A'B'O的位置（点A'在OB上），点B'在反比例函数y = $\frac{k}{x}$的图象上，则k = ________.

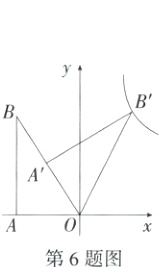
答案：
答案 $\sqrt{3}$
解析 过B'作B'H⊥x轴于H，如图：

∵∠BAO = 90°，AO = 1，OB = 2，
∴∠AOA' = 60°.
∵将△ABO绕点O旋转到△A'B'O的位置，
∴OB' = OB = 2，∠A'OB' = ∠AOA' = 60°，
∴∠B'OH = 180° - ∠AOA' - ∠A'OB' = 60°，
∴OH = $\frac{1}{2}$OB' = 1，B'H = $\frac{\sqrt{3}}{2}$OB' = $\sqrt{3}$，
∴B'(1,$\sqrt{3}$).
∵点B'在反比例函数y = $\frac{k}{x}$的图象上，
∴k = $\sqrt{3}$.

7. [手拉手模型][教材变式·P17T4]如图，以点A为顶点作等腰Rt△ABC，等腰Rt△ADE，其中∠BAC = ∠DAE = 90°，连接BD、CE. 判断BD与CE的位置关系与数量关系，并用旋转的性质说明上述关系成立的理由.（M9223003）

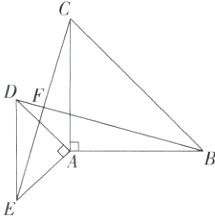
答案： 解析 BD = CE，BD⊥CE.理由：
∵△ABC与△ADE都是等腰直角三角形，且∠BAC = ∠DAE = 90°，
∴将△ACE绕点A顺时针旋转90°后，E与D重合，C与B重合，即△EAC与△DAB重合，
∴CE = BD，∠ACE = ∠ABD，由∠BAC = 90°，易得∠BFC = 90°，即BD⊥CE.
方法解读
本题属于手拉手模型.共顶点，等顶角的两个等腰三角形构成手拉手模型.解有关手拉手模型的问题，通常根据旋转变换及等腰三角形的性质证明三角形全等.