《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

1.(2023浙江绍兴中考)在平面直角坐标系中,将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是(M9223002) ( )
A.(m - 2,n - 1)
B.(m - 2,n + 1)
C.(m + 2,n - 1)
D.(m + 2,n + 1)

答案： 1 D 根据点的坐标的平移规律：横坐标，右移加，左移减；纵坐标，上移加，下移减求解.

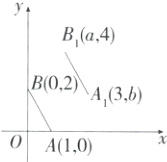
2.(2024北京首师大二附中期中)如图,A(1,0),B(0,2),若将线段AB平移至A₁B₁,则5a - b的值为(M9223002) ( )

A.6
B.8
C.-8
D.10

答案： 2 B
∵A(1,0),B(0,2),A₁(3,b),B₁(a,4),
∴$x_{A₁}-x_{A}=3 - 1 = 2,y_{B₁}-y_{B}=4 - 2 = 2,$
∴线段AB向右平移2个单位，向上平移2个单位得到A₁B₁,
∴$y_{A₁}-y_{A}=b - 0 = 2,x_{B₁}-x_{B}=a - 0 = 2,$则b = 2,a = 2,
∴5a - b = 5×2 - 2 = 8.故选B.

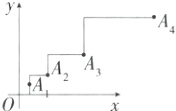
3.新考向·规律探究题 如图,点A₁(1,1),点A₁向上平移1个单位,再向右平移2个单位,得到点A₂,点A₂向上平移2个单位,再向右平移4个单位,得到点A₃,点A₃向上平移4个单位,再向右平移8个单位,得到点A₄,……,按这个规律平移得到点A₁₀₀,则点A₁₀₀的坐标为 ( )

A.(2¹⁰⁰ - 1,2¹⁰⁰)
B.(2⁹⁹,2¹⁰⁰)
C.(2¹⁰⁰ - 1,2⁹⁹)
D.(2⁹⁹ + 1,2¹⁰⁰)

答案： 3 C 点A₁的坐标为(1,1)，点A₂的坐标为(3,2)，点A₃的坐标为(7,4)，点A₄的坐标为(15,8)，……，由此可见，点$A_{n}$的横坐标可表示为$2^{n}-1，$纵坐标可表示为$2^{n - 1}(n$为正整数)，故当n = 100时，点$A_{100}$的坐标为$(2^{100}-1,2^{99}).$故选C.

4.(2024江西中考)在平面直角坐标系中,将点A(1,1)向右平移2个单位长度,再向上平移3个单位长度得到点B,则点B的坐标为_______.

答案： 4 答案 (3,4)
解析 将点A(1,1)向右平移2个单位长度，再向上平移3个单位长度得到点B，则点B的坐标为(1 + 2,1 + 3)，即(3,4).

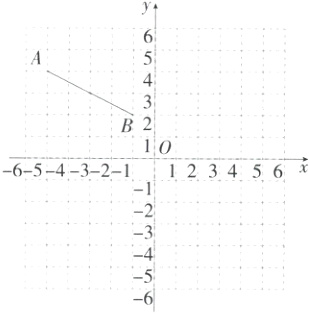
5.(2024北京中央民大附中期中)如图,在平面直角坐标系xOy中,已知点A(-5,4),B(-1,2),将线段AB平移,得到线段CD(点A的对应点为点C,点B的对应点为点D),线段AB上任一点(x,y)平移后的对应点为(x + s,y - t),其中s≥0,t≥0.(M9223002)
(1)若点C与点B恰好重合,则s = _______,t = _______;
(2)若s + t = 5,且平移后三角形BCD的面积最大,则此时s = _______,△BCD的面积为_______.

答案：
5 解析 由题意得C(-5 + s,4 - t),D(-1 + s,2 - t).
(1)
∵点C与点B恰好重合，
∴-5 + s = -1,4 - t = 2,解得s = 4,t = 2.
(2)如图，连接AC.
∵AB//CD,AB = CD,
∴三角形BCD的面积等于三角形ABC的面积.
过C作EF⊥x轴，过A、B作AE⊥EF,BF⊥EF,
∵s + t = 5,
∴$S_{△ABC}=S_{梯形ABFE}-S_{△ACE}-S_{△BCF}=\frac{1}{2}(s + s - 4)×2-\frac{1}{2}st-\frac{1}{2}(2 - t)(s - 4)=s - 2t = 5 - 3t,$
∵t≥0,
∴当t = 0时，面积最大，最大面积为5，此时s = 5.

6.新考向·新定义试题 (2024山东威海中考,7,★☆☆)定义新运算:
①在平面直角坐标系中,|a,b|表示动点从原点出发,沿着x轴正方向(a≥0)或负方向(a＜0)平移|a|个单位长度,再沿着y轴正方向(b≥0)或负方向(b＜0)平移|b|个单位长度.例如,动点从原点出发,沿着x轴负方向平移2个单位长度,再沿着y轴正方向平移1个单位长度,记作|-2,1|.
②加法运算法则:|a,b|+|c,d| = |a + c,b + d|,其中a,b,c,d为实数.
若|3,5|+|m,n| = |-1,2|,则下列结论正确的是 ( )
A.m = 2,n = 7
B.m = -4,n = -3
C.m = 4,n = 3
D.m = -4,n = 3

答案： 6 B 由题意知3 + m = -1,5 + n = 2,
解得m = -4,n = -3.故选B.

7.新考向·新定义试题 (2024河北中考,16,★★☆)平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.
例:“和点”P(2,1)按上述规则连续平移3次后,到达点P₃(2,2),其平移过程如下:
P(2,1) $\xrightarrow[余0]{右}$ P₁(3,1) $\xrightarrow[余1]{上}$ P₂(3,2) $\xrightarrow[余2]{左}$ P₃(2,2).
若“和点”Q按上述规则连续平移16次后,到达点Q₁₆(-1,9),则点Q的坐标为 ( )
A.(6,1)或(7,1)
B.(15,-7)或(8,0)
C.(6,0)或(8,0)
D.(5,1)或(7,1)

答案： D 根据已知点P₃(2,2)的横、纵坐标之和除以3所得的余数为1，继而向上平移1个单位得到P₄(2,3)，此时横、纵坐标之和除以3所得的余数为2，继而向左平移1个单位得到P₅(1,3)，此时横、纵坐标之和除以3所得的余数为1，又向上平移1个单位，……，因此发现规律为若“和点”横、纵坐标之和除以3所得的余数为0时，先向右平移1个单位，再按照向上、向左，向上、向左不断重复的规律平移.若“和点”Q按上述规则连续平移16次后，到达点Q₁₆(-1,9)，则按照“和点”Q₁₆反向运动16次即可，可以分为两种情况：
①Q₁₆先向右平移1个单位得到Q₁₅(0,9)，此时横、纵坐标之和除以3所得的余数为0，应该是Q₁₅向右平移1个单位得到Q₁₆，故矛盾，不成立；②Q₁₆先向下平移1个单位得到Q₁₅(-1,8)，此时横、纵坐标之和除以3所得的余数为1，则应该向上平移1个单位得到Q₁₆，故符合题意，
∴点Q₁₆先向下平移，再向右平移，当平移到第15次时，共计向下平移了8次，向右平移了7次，此时坐标为(-1 + 7,9 - 8)，即(6,1)，
∴最后一次若向右平移则为(7,1)，若向左平移则为(5,1)，故选D.