《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

一、选择题(每小题3分,共24分)
1.(2024北京中考)下列图形中,既是轴对称图形又是中心对称图形的是　(　　)

答案： B。选项A是中心对称图形,不是轴对称图形，选项B 既是轴对称图形又是中心对称图形，选项C既不是轴对称图形也不是中心对称图形，选项D是轴对称图形，不是中心对称图形，故选B.

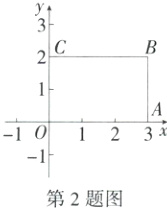
2.(2024黑龙江绥化中考)如图,矩形OABC各顶点分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O为位似中心,将这个矩形按相似比1:3 缩小,则顶点B在第一象限的对应点的坐标是(　　)

A.(9,4)
B.(4,9)
C.(1,$\frac{2}{3}$)
D.(1,$\frac{3}{2}$)

答案： D。
∵以原点O为位似中心，将矩形OABC按相似比1∶3缩小，点B的坐标为(3,2)，
∴顶点B在第一象限的对应点的坐标为(3×$\frac{1}{3}$,2×$\frac{1}{3}$)，即(1,$\frac{2}{3}$)，故选D.

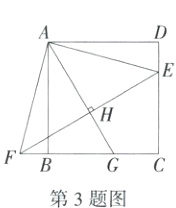
3.(2024北京十一学校期末)如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=6,CG=4,则CE的长为　(　　)

A.2.5
B.7.5
C.8
D.9

答案： B。连接EG，由题意得AE=AF，DE=BF，AG垂直平分FE，所以EG=FG.设CE=x，因为AB=BC=BG+GC=6+4=10，所以DE=10 - x=BF，所以EG=FG=BF+BG=16 - x，由CE²+CG²=EG²，得x²+4²=(16 - x)²，所以x=7.5.故选B.

4.将一片树叶放大,假如这个过程可以看成是在平面直角坐标系中一次无旋转的变换,设变化前树叶尖部点A的坐标为(a,b),变化后得到对应点A'的坐标为(300a + 200,300b - 100),则变化后树叶的面积变为原来的　(　　)
A.300倍
B.3 000倍
C.9 000倍
D.90 000倍

答案： D。
∵点A的坐标为(a,b)，变化后得到对应点A′的坐标为(300a+200,300b - 100)，
∴树叶的边长放大为原来的300倍后再向右平移200个单位长度，向下平移100个单位长度即可得到变化后的树叶，
∴变化后树叶的面积变为原来的300²倍，即90000倍.故选D.

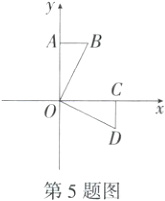
5.(2024四川自贡中考)如图,在平面直角坐标系中,D(4,-2),将Rt△OCD绕点O逆时针旋转90°到△OAB的位置,则点B的坐标为(　　)

A.(2,4)
B.(4,2)
C.(-4,-2)
D.(-2,4)

答案： A。
∵D(4, - 2)，
∴OC=4，CD=2，由题意得OA=OC=4，AB=CD=2，AB⊥y轴，
∴B(2,4)，故选A.

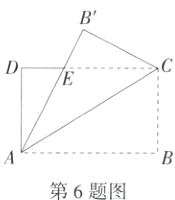
6.(2024四川泸州中考)宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.如图,把黄金矩形ABCD沿对角线AC翻折，点B落在点B'处,AB'交CD于点E,则sin∠DAE的值为　(　　)

A.$\frac{\sqrt{5}}{5}$
B.$\frac{1}{2}$
C.$\frac{3}{5}$
D.$\frac{2\sqrt{5}}{5}$

答案： A。令AD=BC=($\sqrt{5}$ - 1)a，AB=CD=2a，由翻折可知，∠EAC=∠BAC.
∵四边形ABCD是矩形，
∴AB//CD，
∴∠DCA=∠BAC，
∴∠DCA=∠EAC，
∴AE=EC.令DE=x，则AE=EC=2a - x.在Rt△ADE中，由勾股定理得[($\sqrt{5}$ - 1)a]²+x²=(2a - x)²，解得x=$\frac{\sqrt{5} - 1}{2}$a，
∴DE=$\frac{\sqrt{5} - 1}{2}$a，AE=2a - $\frac{\sqrt{5} - 1}{2}$a=$\frac{5 - \sqrt{5}}{2}$a.在Rt△DAE中，sin∠DAE=$\frac{DE}{AE}$=$\frac{\frac{\sqrt{5} - 1}{2}a}{\frac{5 - \sqrt{5}}{2}a}$=$\frac{\sqrt{5}}{5}$.故选A.

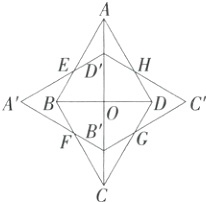
7.(2024北京中考)如图,在菱形ABCD中,∠BAD = 60°,O为对角线的交点.将菱形ABCD绕点O逆时针旋转90°得到菱形A'B'C'D',两个菱形的公共点为E,F,G,H.对八边形BFB'GDHD'E给出下面四个结论:①该八边形各边长都相等;②该八边形各内角都相等;③点O到该八边形各顶点的距离都相等;④点O到该八边形各边所在直线的距离都相等.
其中,所有正确结论的序号是　(　　)

A.①③
B.①④
C.②③
D.②④

答案：
B。分别延长BD，DB，连接OH，
　　　　　　　
∵四边形ABCD是菱形，∠BAD=60°，
∴∠BAO=∠DAO=30°，∠AOD=∠AOB=90°，
∵菱形ABCD绕点O逆时针旋转90°得到菱形A′B′C′D′，
∴点A′，C′在对角线BD所在的直线上，B′，D′在对角线AC上，且OD=OD′=OB=OB′，OA=OA′=OC=OC′，∠D′AH=∠DC′H=30°，
∴AD′=C′D，
∵∠D′HA=∠DHC′，
∴△AD′H≌△C′DH，
∴D′H=DH，
同理可证D′E=BE，BF=B′F，B′G=DG，
∵∠EA′B=∠HC′D=30°，A′B=C′D，∠A′BE=∠C′DH=120°，
∴△A′BE≌△C′DH，
∴DH=BE，
同理可证DG=BF，D′E=B′F.
∴DH=BE=D′H=D′E=BF=FB′=B′G=DG，
∴该八边形各边长都相等，
∴①正确.
易证△OD′H≌△ODH，则∠D′HO=∠DHO，同理可知O为八边形各角平分线的交点，
∴点O到该八边形各边所在直线的距离都相等，
∴④正确.
根据题意，得∠ED′H=120°，
∵∠D′OD=90°，∠OD′H=∠ODH=60°，
∴∠D′HD=150°，
∴该八边形各内角不都相等，
∴②错误.
易得∠DHO=75°，
∴∠ODH≠∠DHO，
故OD≠OH，
∴③错误.
故选B.