《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

1.（2023北京密云期末）在平面直角坐标系xOy中，A(1,3)，B(3, -1)，点P在y轴上，当PA+PB取得最小值时，点P的纵坐标为 （ ）
A.$\frac{4}{3}$
B.$\frac{5}{3}$
C.2
D.$\sqrt{5}$

答案：
C 如图所示，作点A关于y轴的对称点A'，连接BA'交y轴于点P，此时PA + PB = PA' + PB = A'B，根据两点之间，线段最短，可知PA + PB的最小值为A'B的长，此时点P的坐标为(0,2)，
∴点P的纵坐标为2.

2.（数形结合思想）（2023北京朝阳期中）如图，在平面直角坐标系中，点A(-2,2)，B(2,1)，点P(x,0)是x轴上的一个动点.结合图形，得出式子$\sqrt{(x + 2)^{2}+4}+\sqrt{(2 - x)^{2}+1}$的最小值是 （ ）

A.3
B.$\sqrt{17}$
C.5
D.$2\sqrt{2}+\sqrt{5}$

答案：
C
∵P(x,0)，A(-2,2)，B(2,1)，
∴$\sqrt{(x + 2)^2+4}+\sqrt{(2 - x)^2+1}=PA + PB$，即求PA + PB的最小值.
作点B(2,1)关于x轴的对称点B'，连接AB'与x轴交于点P，连接BP，此时PA + PB取得最小值，如图所示.PA + PB = AB'=$\sqrt{3^2+4^2}=5$，
即$\sqrt{(x + 2)^2+4}+\sqrt{(2 - x)^2+1}$的最小值为5.

3.（2024北京门头沟大峪中学期中）如图，正方形ABCD的边长为4，点E在AB上，且BE = 1，F为对角线AC上一动点，则△BFE周长的最小值为______.

答案：
答案 6
解析 如图，连接ED交AC于点F，连接BF，
∵四边形ABCD是正方形，
∴点B与点D关于对角线AC对称，
∴BF = DF，
∴△BFE的周长 = BF + EF + BE = DE + BE，此时△BEF的周长最小，
∵正方形ABCD的边长为4，
∴AD = AB = 4，∠DAB = 90°，
∵点E在AB上且BE = 1，
∴AE = 3，
∴DE=$\sqrt{AD^2+AE^2}=5$，
∴△BFE的周长 = 5 + 1 = 6.

4.（2024北京丰台期中）如图，在△ABC中，AD是BC边上的高，已知BD = 1，AD = CD = 2，BC上方有一动点P，且点P到A，D两点的距离相等，则△BCP周长的最小值为______.

答案：
答案 $\sqrt{13}+3$
解析
∵点P到A，D两点的距离相等，
∴点P在AD的垂直平分线l上.作B点关于l的对称点B'，连接B'C交l于点P，
∴BP = B'P，
∴BP + CP = B'P + CP = B'C，此时△BCP的周长最小，
∵AD⊥BC，BD = 1，AD = CD = 2，
∴BB' = 2，BC = 3.
在Rt△BCB'中，B'C=$\sqrt{BC^2+B'B^2}=\sqrt{9 + 4}=\sqrt{13}$，
∴△BCP周长的最小值为$\sqrt{13}+3$.

5.如图，抛物线y = ax²+2x - 3a经过A(1,0)、B(b,0)、C(0,c)三点.
(1)求b，c的值；
(2)在抛物线的对称轴上找一点P，使PA+PC的值最小，求点P的坐标.

答案：
解析
(1)把A(1,0)代入y = ax² + 2x - 3a，得a + 2 - 3a = 0，解得a = 1，
∴抛物线的解析式为y = x² + 2x - 3.
把B(b,0)，C(0,c)代入y = x² + 2x - 3，
得b = 1或b = -3，c = -3，
∵A(1,0)，
∴b = -3.
(2)
∵抛物线的解析式为y = x² + 2x - 3，
∴对称轴为直线x = -$\frac{2}{2}=-1$，
连接BC，交抛物线的对称轴于点P，连接PA，此时PA + PC的值最小，如图所示：

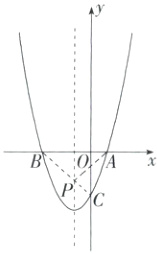
设直线BC的解析式为y = kx + m(k≠0)，将B(-3,0)，C(0,-3)代入得$\begin{cases}-3k + m = 0\\m = -3\end{cases}$，解得$\begin{cases}k = -1\\m = -3\end{cases}$，
∴直线BC的解析式为y = -x - 3，当x = -1时，y = 1 - 3 = -2，
∴P(-1,-2).