第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1. 教材变式·P74例3(2023湖北恩施州中考)县林业部门考察银杏树苗在一定条件下移植的成活率,所统计的银杏树苗移植成活的相关数据如下表:(M9225004)
|移植的棵数a|100|300|600|1 000|7 000|15 000|
|----|----|----|----|----|----|----|
|成活的棵数b|84|279|505|847|6 337|13 581|
|成活的频率$\frac{b}{a}|0.84|0.93|0.842|0.847|0.905|0.905|$
根据表中的信息,估计银杏树苗在一定条件下移植成活的概率为(精确到0.1) ( )
A.0.905
B.0.90
C.0.9
D.0.8
|移植的棵数a|100|300|600|1 000|7 000|15 000|
|----|----|----|----|----|----|----|
|成活的棵数b|84|279|505|847|6 337|13 581|
|成活的频率$\frac{b}{a}|0.84|0.93|0.842|0.847|0.905|0.905|$
根据表中的信息,估计银杏树苗在一定条件下移植成活的概率为(精确到0.1) ( )
A.0.905
B.0.90
C.0.9
D.0.8
答案:
C 由表格数据可得,随着移植棵数的增加,树苗移植成活的频率稳定在0.9左右,故估计银杏树苗在一定条件下移植成活的概率为0.9.故选C.
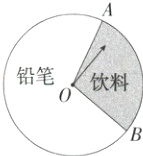
2. 如图,为了鼓励消费,某商场设置一个可以自由转动的转盘.规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针指向哪个区域顾客就获得相应的奖品.下表是活动进行中的一组统计数据:
|转动转盘的次数n|100|150|200|500|800|1 000|
|----|----|----|----|----|----|----|
|落在“饮料”区域的次数m|32|39|64|155|254|299|
则估计转盘中“饮料”区域的圆心角∠AOB的度数是(M9225004) ( )
A.119°
B.108°
C.87°
D.90°
|转动转盘的次数n|100|150|200|500|800|1 000|
|----|----|----|----|----|----|----|
|落在“饮料”区域的次数m|32|39|64|155|254|299|
则估计转盘中“饮料”区域的圆心角∠AOB的度数是(M9225004) ( )

A.119°
B.108°
C.87°
D.90°
答案:
B 转动转盘一次,可估计指针落在“饮料”区域的概率为0.3,所以估计转盘中“饮料”区域的圆心角∠AOB的度数是360°×0.3 = 108°.故选B.
3. 新独家原创 某生物实验小组对某品种绿豆发芽情况进行测试,在测试条件相同的情况下,得到如下数据:
|绿豆粒数|100|300|800|1 000|2 000|3 000|
|----|----|----|----|----|----|----|
|发芽绿豆的粒数|96|287|770|958|1 923|a|
则a的值最有可能是(M9225004) ( )
A.2 700
B.2 780
C.2 880
D.2 940
|绿豆粒数|100|300|800|1 000|2 000|3 000|
|----|----|----|----|----|----|----|
|发芽绿豆的粒数|96|287|770|958|1 923|a|
则a的值最有可能是(M9225004) ( )
A.2 700
B.2 780
C.2 880
D.2 940
答案:
C
∵96÷100 = 0.96,287÷300≈0.9567,770÷800 = 0.9625,958÷1000 = 0.958,1923÷2000 = 0.9615,
∴可估计该品种绿豆发芽的概率为0.96,则a的值最有可能是3000×0.96 = 2880.故选C.
∵96÷100 = 0.96,287÷300≈0.9567,770÷800 = 0.9625,958÷1000 = 0.958,1923÷2000 = 0.9615,
∴可估计该品种绿豆发芽的概率为0.96,则a的值最有可能是3000×0.96 = 2880.故选C.
4. 在某数控车床加工中心,质检员每天要对加工的每一个零件尺寸进行检测,质检员对某天生产的15个零件进行了测量,测量数据按照由小到大的顺序进行整理如下表:
|编号|①|②|③|④|⑤|⑥|⑦|⑧|⑨|⑩|⑪|⑫|⑬|⑭|⑮|
|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|
|尺寸/mm|47.8|48.6|49.1|49.2|49.4|49.6|49.7|a|50.1|50.3|50.4|50.6|50.7|50.8|b|
按照生产标准,产品等次规定如下表:(注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)计算在内)
|尺寸/mm|产品等次|
|----|----|
|49.7≤x≤50.3|特等品|
|49.5≤x≤50.5|优等品|
|49.0≤x≤51.0|合格品|
|x<49.0或x>51.0|残次品|
(1)已知此次抽检的合格率为80%,请判断编号为⑮的产品是不是合格品,并说明理由.
(2)已知此次抽检出的优等品尺寸的中位数为50.0 mm.
①求a的值;
②将这些优等品分成两组,一组尺寸大于50.0 mm,另一组尺寸不大于50.0 mm,从这两组中各随机抽取1件进行复检,请用列表或画树状图的方法求出抽到的2件产品都是特等品的概率.
|编号|①|②|③|④|⑤|⑥|⑦|⑧|⑨|⑩|⑪|⑫|⑬|⑭|⑮|
|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|
|尺寸/mm|47.8|48.6|49.1|49.2|49.4|49.6|49.7|a|50.1|50.3|50.4|50.6|50.7|50.8|b|
按照生产标准,产品等次规定如下表:(注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)计算在内)
|尺寸/mm|产品等次|
|----|----|
|49.7≤x≤50.3|特等品|
|49.5≤x≤50.5|优等品|
|49.0≤x≤51.0|合格品|
|x<49.0或x>51.0|残次品|
(1)已知此次抽检的合格率为80%,请判断编号为⑮的产品是不是合格品,并说明理由.
(2)已知此次抽检出的优等品尺寸的中位数为50.0 mm.
①求a的值;
②将这些优等品分成两组,一组尺寸大于50.0 mm,另一组尺寸不大于50.0 mm,从这两组中各随机抽取1件进行复检,请用列表或画树状图的方法求出抽到的2件产品都是特等品的概率.
答案:
解析
(1)
∵抽检的合格率为80%,
∴合格品有15×80% = 12(个),则残次品有3个,而从编号①至编号⑭对应的产品中,只有编号①与编号②对应的产品为残次品,故编号为⑮的产品不是合格品.
(2)①按照优等品的标准,编号⑥到编号⑪对应的6个产品为优等品,中间两个产品的尺寸分别为50.1mm和amm,
∴$\frac{50.1 + a}{2}$ = 50.0,解得a = 49.9.
②在优等品中,编号⑥⑦⑧对应的产品尺寸不大于50.0mm,分别记为A₁,A₂,A₃;编号⑨⑩⑪对应的产品尺寸大于50.0mm,分别记为B₁,B₂,B₃,其中的特等品为A₂,A₃,B₁,B₂.根据题意列表:
| | B₁ | B₂ | B₃ |
| ---- | ---- | ---- | ---- |
| A₁ | (A₁,B₁) | (A₁,B₂) | (A₁,B₃) |
| A₂ | (A₂,B₁) | (A₂,B₂) | (A₂,B₃) |
| A₃ | (A₃,B₁) | (A₃,B₂) | (A₃,B₃) |
由上表可知共有9种等可能的结果,其中2件产品都是特等品的结果有4种,所以抽到的2件产品都是特等品的概率为$\frac{4}{9}$.
(1)
∵抽检的合格率为80%,
∴合格品有15×80% = 12(个),则残次品有3个,而从编号①至编号⑭对应的产品中,只有编号①与编号②对应的产品为残次品,故编号为⑮的产品不是合格品.
(2)①按照优等品的标准,编号⑥到编号⑪对应的6个产品为优等品,中间两个产品的尺寸分别为50.1mm和amm,
∴$\frac{50.1 + a}{2}$ = 50.0,解得a = 49.9.
②在优等品中,编号⑥⑦⑧对应的产品尺寸不大于50.0mm,分别记为A₁,A₂,A₃;编号⑨⑩⑪对应的产品尺寸大于50.0mm,分别记为B₁,B₂,B₃,其中的特等品为A₂,A₃,B₁,B₂.根据题意列表:
| | B₁ | B₂ | B₃ |
| ---- | ---- | ---- | ---- |
| A₁ | (A₁,B₁) | (A₁,B₂) | (A₁,B₃) |
| A₂ | (A₂,B₁) | (A₂,B₂) | (A₂,B₃) |
| A₃ | (A₃,B₁) | (A₃,B₂) | (A₃,B₃) |
由上表可知共有9种等可能的结果,其中2件产品都是特等品的结果有4种,所以抽到的2件产品都是特等品的概率为$\frac{4}{9}$.
查看更多完整答案,请扫码查看


