《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

7.（2024北京二中教育集团月考，16，★☆☆）小亮有黑色、白色卡片各10张，分别写有数字0~9. 把它们像扑克牌那样洗过后，数字朝下，排成四行，排列规则如下：
①从左至右按从小到大的顺序排列；
②黑色、白色卡片数字相同时，黑色卡片放在左边.
小亮每行翻开了两张卡片，如图所示，小亮让小明根据排列规则推算其余卡片上的数字，小明发现有的卡片上的数字可以唯一确定，例如，第四行最后一张白色卡片上的数字只能是______，有的卡片上的数字并不能唯一确定，小明对不能唯一确定的卡片上的数字进行猜测，则小明一次猜对所有数字的概率是______.

答案： 答案$8;\frac{1}{3}$
解析
∵ 黑色卡片8在第四行最后一张白色卡片的左边，
∴ 第四行最后一张白色卡片上的数字可能为8或9，又
∵ 白色卡片9排在第一行，
∴ 第四行最后一张白色卡片上的数字只能是8。每行能确定的数字为第一行：15679；第二行：1_345；第三行：0_679；第四行：02_88。不能确定的是黑色卡片2，3和4，共有三种填法，每种填法是等可能的，其中猜对的有一种，故所求概率为$\frac{1}{3}$。

例 一般地，如果在一次实验中，结果落在区域D中的每一点都是等可能的，用A表示“实验结果落在区域D中的一个小区域M”这个事件，那么事件A发生的概率P(A) = $\frac{M的面积}{D的面积}$，如图所示的是一个正方形及其内切圆，随机向正方形内投一粒米，落在圆内的概率为______.

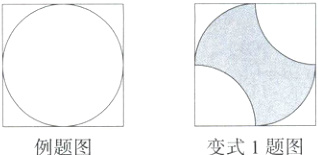
答案： 答案$\frac{\pi}{4}$
解析 设正方形的边长为2a，
则P(随机向正方形内投一粒米，落在圆内)=$\frac{\pi a^{2}}{4a^{2}}=\frac{\pi}{4}$。

变式
1. 改为不规则图形（2023山东烟台中考）如图，在正方形中，阴影部分是以正方形的顶点及其对称中心为圆心，以正方形边长的一半为半径作弧形成的封闭图形. 让一个小球在该正方形内自由滚动，小球随机地停在正方形内的某一点上. 若小球停在阴影部分的概率为P1，停在空白部分的概率为P2，则P1与P2的大小关系为（ ）

A. P1 ＜ P2
B. P1 = P2
C. P1 ＞ P2
D. 无法判断

答案： B　令正方形的边长为2a，则空白部分的面积为
$2\times\frac{1}{4}\times\pi\cdot a^{2}+2\left(a^{2}-\frac{1}{4}\times\pi\cdot a^{2}\right)=\frac{1}{2}\pi a^{2}+2a^{2}-\frac{1}{2}\pi a^{2}=2a^{2}$，则阴影部分的面积为$(2a)^{2}-2a^{2}=4a^{2}-2a^{2}=2a^{2}$，
所以小球停在阴影部分的概率$P_{1}=$停在空白部分的概率$P_{2}$，故选B。

2. 改为转盘 一个可以自由转动且质地均匀的转盘被分成6个大小相同的扇形. 在转盘的适当地方涂上灰色，未涂色部分为白色. 为了使转动的转盘停止时，指针指向灰色的概率为$\frac{2}{3}$，则下列各图中涂色方案正确的是（ ）

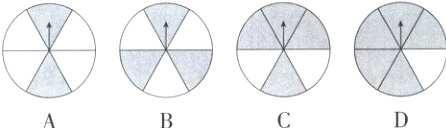
答案： C。选项A，指针指向灰色的概率为$2\div6=\frac{1}{3}$；选项B，指针指向灰色的概率为$3\div6=\frac{1}{2}$；选项C，指针指向灰色的概率为$4\div6=\frac{2}{3}$；选项D，指针指向灰色的概率为$5\div6=\frac{5}{6}$。故选C。

8. 应用意识 取一根长度为4米的绳子，在任意位置剪断，求剪得的两段绳子都不少于1米的概率.（M9225001）

答案： 解析
∵ 绳子的总长为4米，剪得的两段绳子的长都不小于1米，
∴ 如图所示，只能在中间2米的部分剪断，才能使剪得的两段绳子符合条件，
1米 2米 1米
∴ 剪得的两段绳子都不少于1米的概率=$\frac{1}{2}$。