《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

8.(2024辽宁中考,12,★☆☆)在平面直角坐标系中,线段AB的端点分别为A(2,-1),B(1,0),将线段AB平移后,点A的对应点A'的坐标为(2,1),则点B的对应点B'的坐标为_______.

答案： 8 答案 (1,2)
解析
∵A(2,-1),A'(2,1),
∴平移规律是向上平移2个单位，
∵B(1,0),
∴B'(1,2).

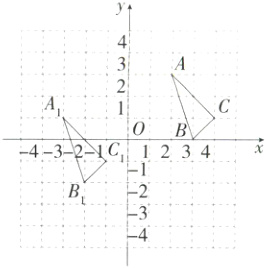
9.(2024北京四十四中期中,25,★★☆)三角形ABC与三角形A₁B₁C₁在平面直角坐标系中的位置如图所示.(M9223002)
(1)分别写出下列各点的坐标:
A_______;B_______;C_______.
(2)三角形ABC是由三角形A₁B₁C₁向_______平移_______个单位,再向_______平移_______个单位得到的.
(3)若点P(x,y)是三角形ABC内部一点,则三角形A₁B₁C₁内部的对应点P'的坐标为_______(用x和y表示).
(4)直接写出三角形ABC的面积:_______.

答案： 9 解析
(1)A(2,3),B(3,0),C(4,1).
(2)三角形ABC是由三角形A₁B₁C₁向右平移5个单位，再向上平移2个单位得到的.
(3)点P'的坐标为(x - 5,y - 2).
(4)三角形ABC的面积为$3×2-\frac{1}{2}×1×3-\frac{1}{2}×2×2-\frac{1}{2}×1×1 = 2.$

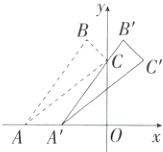
10.运算能力 如图,△ABC的顶点A(-4,0),B(-1,4),点C在y轴的正半轴上,AB = AC,将△ABC向右平移得到△A'B'C',若线段A'B'经过点C,则点B'的坐标为 ( )

A.($\frac{3}{4}$,3)
B.($\frac{7}{4}$,3)
C.($\frac{3}{4}$,4)
D.($\frac{7}{4}$,4)

答案： 10 C 设直线AB的解析式为y = kx + b,
把A(-4,0),B(-1,4)分别代入解析式，
得$\begin{cases}-4k + b = 0\\-k + b = 4\end{cases}，$解得$\begin{cases}k=\frac{4}{3}\\b=\frac{16}{3}\end{cases}，$
∴直线AB的解析式为$y=\frac{4}{3}x+\frac{16}{3}.$
∵A(-4,0),B(-1,4)，
∴$AB=\sqrt{(-4 + 1)^{2}+4^{2}} = 5,$
∴AC = AB = 5,
∵OA = 4,
∴$OC=\sqrt{5^{2}-4^{2}} = 3,$
∴C(0,3).
∵A'B'//AB,
∴直线A'B'的解析式为$y=\frac{4}{3}x + 3,$令y = 0,则$x=-\frac{9}{4},$
∴$A'(-\frac{9}{4},0).$连接BB'，则$BB' = AA' = 4-\frac{9}{4}=\frac{7}{4},\frac{7}{4}-1=\frac{3}{4},$
∴$B'(\frac{3}{4},4).$故选C.

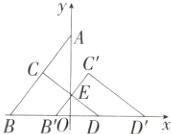
11.推理能力 (2024河南洛阳一模)如图,在平面直角坐标系中,Rt△OAB的顶点O为坐标原点,A(0,8),B(-6,0),C是斜边AB的中点,且DC⊥AB交x轴于点D.将△BCD沿x轴向右平移得到△B'C'D',当B'C'的中点E恰好落在y轴上时,点D'的坐标为 ( )

A.($\frac{41}{6}$,0)
B.($\frac{13}{2}$,0)
C.($\frac{77}{6}$,0)
D.(7,0)

答案：
11 A
∵点A的坐标为(0,8)，点B的坐标为(-6,0)，且点C为AB的中点，
∴OB = 6,OA = 8，点C的坐标为(-3,4).在Rt△ABO中，$AB=\sqrt{6^{2}+8^{2}} = 10,$
∴$BC=\frac{1}{2}AB = 5.$令BC的中点为H，则点H的坐标为$(-\frac{9}{2},2).$
由题意得，平移后点H落在y轴上的点E处，
∴△BCD向右平移了$\frac{9}{2}$个单位长度.
∵CD⊥AB,∠AOD = 90°,
∴∠BAO = ∠CDB.在Rt△ABO中，$sin∠BAO=\frac{BO}{AB}=\frac{3}{5},$
∴$sin∠CDB=\frac{3}{5}.$在Rt△BCD中，$sin∠CDB=\frac{BC}{BD},$
∴$\frac{5}{BD}=\frac{3}{5},$
∴$BD=\frac{25}{3},$
∵$-6+\frac{25}{3}=\frac{7}{3},$
∴点D的坐标为$(\frac{7}{3},0),$
∵$\frac{7}{3}+\frac{9}{2}=\frac{41}{6},$
∴点D'的坐标为$(\frac{41}{6},0).$故选A.