第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.(2024北京通州期末)某校准备选派甲、乙、丙、丁中的一名队员代表学校参加全区的跳绳比赛,下表为四名队员选拔赛成绩的平均数和方差,你觉得成绩好且发挥稳定的队员是(M9226003)( )
| |甲|乙|丙|丁|
|--|--|--|--|--|
|平均数|201|180|201|180|
|方差|13|5.5|2.4|2.5|
A.甲
B.乙
C.丙
D.丁
| |甲|乙|丙|丁|
|--|--|--|--|--|
|平均数|201|180|201|180|
|方差|13|5.5|2.4|2.5|
A.甲
B.乙
C.丙
D.丁
答案:
C
∵ 甲、丙成绩的平均数大于乙、丁成绩的平均数,
∴ 从甲和丙中选择一人参加比赛,
∵ $s_{甲}^{2}>s_{丙}^{2}$,
∴ 选择丙参赛. 故选 C.
∵ 甲、丙成绩的平均数大于乙、丁成绩的平均数,
∴ 从甲和丙中选择一人参加比赛,
∵ $s_{甲}^{2}>s_{丙}^{2}$,
∴ 选择丙参赛. 故选 C.
2.(2022贵州铜仁中考)为了增强学生的安全防范意识,某校初三(1)班举行了一次安全知识抢答赛,抢答题一共20个,记分规则如下:每答对一题得5分,每答错或不答一题扣1分.小红一共得70分,则小红答对的题的个数为( )
A.14
B.15
C.16
D.17
A.14
B.15
C.16
D.17
答案:
B 设小红答对的题的个数为 $x$,由题意得 $5x-(20 - x)=70$,解得 $x = 15$,故选 B.
3.(2023北京东城广渠门中学一检)如图,用绳子围成周长为10m的矩形,记矩形的一边长为xm,其邻边长为ym,矩形的面积为Sm².当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是
( )

A.一次函数关系,二次函数关系
B.正比例函数关系,二次函数关系
C.二次函数关系,正比例函数关系
D.二次函数关系,一次函数关系
( )

A.一次函数关系,二次函数关系
B.正比例函数关系,二次函数关系
C.二次函数关系,正比例函数关系
D.二次函数关系,一次函数关系
答案:
A 由题意得 $2(x + y)=10$,
∴ $x + y = 5$,
∴ $y = 5 - x$,即 $y$ 与 $x$ 满足一次函数关系,
∵ $S = xy = x(5 - x)=-x^{2}+5x$,
∴ $S$ 与 $x$ 满足二次函数关系,故选 A.
∴ $x + y = 5$,
∴ $y = 5 - x$,即 $y$ 与 $x$ 满足一次函数关系,
∵ $S = xy = x(5 - x)=-x^{2}+5x$,
∴ $S$ 与 $x$ 满足二次函数关系,故选 A.
4.(2023北京大兴期末)某超市推出如下优惠方案:
(1)一次性购物不超过100元,不享受优惠;
(2)一次性购物超过100元,但不超过350元,一律9折;
(3)一次性购物超过350元,一律8折.王波两次购物分别付款80元、288元,如果他将这两次所购物品一次性购买,则应付款(M9226002)
( )
A.320元
B.332元
C.320元或352元
D.332元或363元
(1)一次性购物不超过100元,不享受优惠;
(2)一次性购物超过100元,但不超过350元,一律9折;
(3)一次性购物超过350元,一律8折.王波两次购物分别付款80元、288元,如果他将这两次所购物品一次性购买,则应付款(M9226002)
( )
A.320元
B.332元
C.320元或352元
D.332元或363元
答案:
C ①若第二次购物超过 100 元,但不超过 350 元,设此时所购物品价格为 $x$ 元,则 $90\%x = 288$,解得 $x = 320$,则两次所购物品价格为 $80 + 320 = 400$ 元,因为 $400>350$,所以一次性购买享受 8 折优惠,因此王波应付 $400×80\% = 320$(元);②若第二次购物超过 350 元,设此时所购物品价格为 $y$ 元,则 $80\%y = 288$,解得 $y = 360$,则两次所购物品价格为 $80 + 360 = 440$ 元,因为 $440>350$,所以一次性购买享受 8 折优惠,因此王波应付 $440×80\% = 352$(元).
5.如图,某一时刻的太阳光下,小明测得一棵树落在地面上的影长为2.8米,落在墙上的影子高为1.2米,同一时刻同一地点,身高1.6米的小明在阳光下的影长为0.4米,则这棵树的高为( )
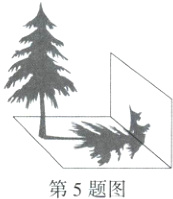
A.6.2米
B.10米
C.11.2米
D.12.4米

A.6.2米
B.10米
C.11.2米
D.12.4米
答案:
D 设从墙上的影子的顶端到树的顶端的垂直高度是 $x$ 米,则 $\frac{1.6}{0.4}=\frac{x}{2.8}$,解得 $x = 11.2$. 所以树的高度 = $11.2 + 1.2 = 12.4$(米),故选 D.
6.(2023黑龙江佳木斯中考)某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有 ( )
A.5种
B.6种
C.7种
D.8种
A.5种
B.6种
C.7种
D.8种
答案:
B 当购买 5 本 $A$ 种图书时,设购买 $x$ 本 $B$ 种图书,$y$ 本 $C$ 种图书,根据题意,得 $30×5 + 25x + 20y = 500$,
∴ $x = 14-\frac{4}{5}y$,又
∵ $x$,$y$ 均为正整数,
∴ $\begin{cases}x = 10\\y = 5\end{cases}$ 或 $\begin{cases}x = 6\\y = 10\end{cases}$ 或 $\begin{cases}x = 2\\y = 15\end{cases}$,
∴ 当购买 5 本 $A$ 种图书时,有 3 种采购方案;
当购买 6 本 $A$ 种图书时,设购买 $m$ 本 $B$ 种图书,$n$ 本 $C$ 种图书,根据题意,得 $30×6 + 25m + 20n = 500$,
∴ $n = 16-\frac{5}{4}m$,又
∵ $m$,$n$ 均为正整数,
∴ $\begin{cases}m = 4\\n = 11\end{cases}$ 或 $\begin{cases}m = 8\\n = 6\end{cases}$ 或 $\begin{cases}m = 12\\n = 1\end{cases}$,
∴ 当购买 6 本 $A$ 种图书时,有 3 种采购方案.
∴ 此次采购的方案有 $3 + 3 = 6$(种).
∴ $x = 14-\frac{4}{5}y$,又
∵ $x$,$y$ 均为正整数,
∴ $\begin{cases}x = 10\\y = 5\end{cases}$ 或 $\begin{cases}x = 6\\y = 10\end{cases}$ 或 $\begin{cases}x = 2\\y = 15\end{cases}$,
∴ 当购买 5 本 $A$ 种图书时,有 3 种采购方案;
当购买 6 本 $A$ 种图书时,设购买 $m$ 本 $B$ 种图书,$n$ 本 $C$ 种图书,根据题意,得 $30×6 + 25m + 20n = 500$,
∴ $n = 16-\frac{5}{4}m$,又
∵ $m$,$n$ 均为正整数,
∴ $\begin{cases}m = 4\\n = 11\end{cases}$ 或 $\begin{cases}m = 8\\n = 6\end{cases}$ 或 $\begin{cases}m = 12\\n = 1\end{cases}$,
∴ 当购买 6 本 $A$ 种图书时,有 3 种采购方案.
∴ 此次采购的方案有 $3 + 3 = 6$(种).
7.(2024吉林长春二模)图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC = 40cm,α = 37°,则双翼边缘端点C与D之间的距离为 ( )
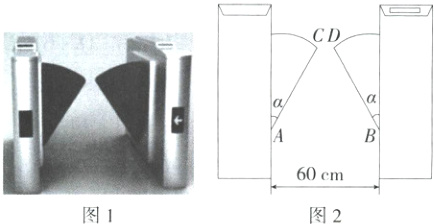
A.(60 - 40sin37°)cm
B.(60 - 2×40cos37°)cm
C.(60 - 2×40tan37°)cm
D.(60 - 2×40sin37°)cm

A.(60 - 40sin37°)cm
B.(60 - 2×40cos37°)cm
C.(60 - 2×40tan37°)cm
D.(60 - 2×40sin37°)cm
答案:
D 如图,作直线 $CD$,交双翼闸机于点 $E$、$F$,则 $CE\perp AE$,$DF\perp BF$,
由题意可得 $CE = DF$,$EF = 60$ cm,
在直角三角形 $ACE$ 中,$CE = AC\cdot\sin37^{\circ}=40\sin37^{\circ}$ cm,
∴ $CD = EF - 2CE=(60 - 2×40\sin37^{\circ})$ cm. 故选 D.
由题意可得 $CE = DF$,$EF = 60$ cm,
在直角三角形 $ACE$ 中,$CE = AC\cdot\sin37^{\circ}=40\sin37^{\circ}$ cm,
∴ $CD = EF - 2CE=(60 - 2×40\sin37^{\circ})$ cm. 故选 D.
查看更多完整答案,请扫码查看


