《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

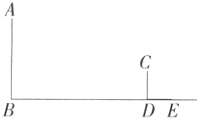
4.(2023山东枣庄期末)小红想利用阳光下的影长测量学校旗杆AB的高度.如图,某一时刻,她在地面上竖直放置了一个2米长的标杆CD,测得其影长DE=1.4米.(M9224001)
(1)请在图中画出此时旗杆AB在阳光下的投影BF;
(2)如果BF=5.6米,求旗杆AB的高.

答案：
解析
(1)如图，连接CE，过A点作AF//CE交BD于F，则BF即为所求.

(2)
∵AF//CE，
∴∠AFB = ∠CED，
又
∵∠ABF = ∠CDE = 90°，
∴△ABF∽△CDE
∴$\frac{AB}{CD}=\frac{BF}{DE}$，即$\frac{AB}{2}=\frac{5.6}{1.4}$，
∴AB = 8 m.
答：旗杆AB的高为8 m.

5.(2023北京海淀二模,2,★☆☆)一个正五棱柱按如图所示的方式摆放,光线由上到下照射此正五棱柱时的正投影是(M9224001) ( )
  

答案： B 光线由上向下照射正五棱柱时的正投影是正五边形.故选B.

6.(2024四川凉山州中考,11,★★☆)如图,一块面积为60 cm²的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A₁B₁C₁,若OB∶BB₁=2∶3,则△A₁B₁C₁的面积是(M9224001) ( )

A.90 cm²
B.135 cm²
C.150 cm²
D.375 cm²

答案： D 由题意可知，△ABC与△A₁B₁C₁是位似图形，且△ABC与△A₁B₁C₁的相似比为$\frac{2}{2 + 3}=\frac{2}{5}$，
∴△A₁B₁C₁的面积是60÷$(\frac{2}{5})^2$= 375(cm²)，故选D.

7.应用意识 某数学兴趣小组利用树影测量树高,如图,已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°角.(√2≈1.41,√3≈1.73,√6≈2.45,结果精确到0.1米)
(1)求树AB的高.
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倒下过程中,树影长度发生了变化,假设太阳光线与地面的夹角保持不变.
①求树与地面成45°角时的影长;
②求树的最大影长.

答案：
解析
(1)AB = AC·tan 30° = 12×$\frac{\sqrt{3}}{3}$= 4$\sqrt{3}$≈4×1.73≈6.9(米).
故树AB的高约为6.9米.
(2)①如图，作B₁N⊥AC₁于N，
∴AN = B₁N = AB₁·sin 45° = 4$\sqrt{3}$×$\frac{\sqrt{2}}{2}$= 2$\sqrt{6}$(米)，
∴$NC_1=\frac{NB_1}{\tan30^{\circ}}=\frac{2\sqrt{6}}{\frac{\sqrt{3}}{3}} = 6\sqrt{2}$(米)，
∴AC₁ = AN + NC₁ = 2$\sqrt{6}$+ 6$\sqrt{2}$≈2×2.45 + 6×1.41≈13.4(米).
故树与地面成45°角时的影长约为13.4米.

②如图，当树与光线垂直(即树在AB₂的位置)时，影长最大，为AC₂的长度.
∵∠AC₂B₂ = 30°，AB₂ = 4$\sqrt{3}$米，
∴AC₂ = 2AB₂ = 8$\sqrt{3}$≈8×1.73≈13.8(米).
故树的最大影长约为13.8米.