《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

15.(2024北京中考,21,★☆☆)为防治污染,保护和改善生态环境,自2023年7月1日起,我国全面实施汽车国六排放标准6b阶段(以下简称“标准”).对某型号汽车,“标准”要求A类物质排放量不超过35 mg/km,A,B两类物质排放量之和不超过50 mg/km.
已知该型号某汽车的A,B两类物质排放量之和原为92 mg/km.经过一次技术改进,该汽车的A类物质排放量降低了50%,B类物质排放量降低了75%,A,B两类物质排放量之和为40 mg/km.判断这次技术改进后该汽车的A类物质排放量是否符合“标准”,并说明理由.(M9226001)

答案： 解析 符合，理由如下：
设技术改进后该汽车的A类物质排放量为x mg/km，则B类物质排放量为(40 - x)mg/km，
由题意得$\frac{x}{1 - 50\%}+\frac{40 - x}{1 - 75\%}=92$，解得x = 34，
∵34＜35，
∴这次技术改进后该汽车的A类物质排放量符合“标准”.

16.北京人文·冬奥会 (2022北京中考,25,★☆☆)单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.运动员起跳后的飞行路线可以看成是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x - h)² + k(a ＜ 0).(M9226002)

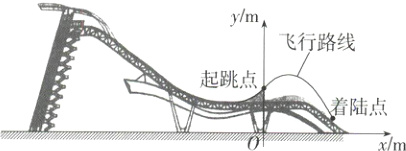
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下表:
|水平距离x/m|0|2|5|8|11|14|
|----|----|----|----|----|----|----|
|竖直高度y/m|20.00|21.40|22.75|23.20|22.75|21.40|
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系式y = a(x - h)² + k(a ＜ 0).
(2)第二次训练时,该运动员的竖直高度y与水平距离x近似满足函数关系y = - 0.04(x - 9)² + 23.24.记该运动员第一次训练的着陆点的水平距离为d₁,第二次训练的着陆点的水平距离为d₂,则d₁______d₂(填“＞”“=”或“＜”).

答案： 解析
(1)根据表格中的数据可知，抛物线的顶点坐标为(8，23.20)，
∴h = 8，k = 23.20，
即该运动员竖直高度的最大值为23.20 m，
将(0，20.00)代入$y = a(x - 8)^{2}+23.20$得，
$20.00 = a(0 - 8)^{2}+23.20$，解得$a = - 0.05$，
∴函数关系式为$y = - 0.05(x - 8)^{2}+23.20$.
(2)设第一次训练时，着陆点的纵坐标为t，
则$t = - 0.05(x - 8)^{2}+23.20$，
解得$x = 8+\sqrt{20(23.20 - t)}$或$x = 8-\sqrt{20(23.20 - t)}$，
根据图象可知，第一次训练时着陆点的水平距离$d_1=(8+\sqrt{20(23.20 - t)})$m.
第二次训练时，令y = t，则$t = - 0.04(x - 9)^{2}+23.24$，
解得$x = 9+\sqrt{25(23.24 - t)}$或$x = 9-\sqrt{25(23.24 - t)}$，
根据图象可知，第二次训练时，当运动员竖直高度为t m时，水平距离$d_2=(9+\sqrt{25(23.24 - t)})$m，
∵$0＜20(23.20 - t)＜25(23.24 - t)$，
∴$\sqrt{20(23.20 - t)}＜\sqrt{25(23.24 - t)}$，
∴$8+\sqrt{20(23.20 - t)}＜9+\sqrt{25(23.24 - t)}$，
即第一次训练时着陆点的水平距离小于第二次训练时着陆点的水平距离，
∴$d_1＜d_2$.