《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

二、填空题(每小题4分,共24分)
9.从5张上面分别写着“学”“生”“学”“数”“学”的卡片(大小、形状完全相同)中随机抽取一张,则这张卡片上面恰好写着“数”字的概率是________.

答案： 答案 $\frac{1}{5}$
解析
∵5张卡片中有1张写有“数”字，
∴抽取一张恰好写有“数”字的概率为$\frac{1}{5}$.

10.(2024北京清华大学附中上地学校月考)为了解北京市九年级学生的1分钟跳绳成绩,随机抽取了1 000名学生的1分钟跳绳成绩,统计如下表.根据北京市体育中考跳绳评分标准,1分钟跳绳个数不小于180的为满分,现任意抽查北京市一名九年级学生,1分钟跳绳成绩为满分的概率约为________.

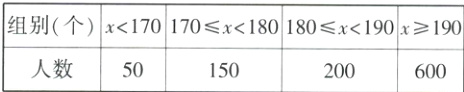
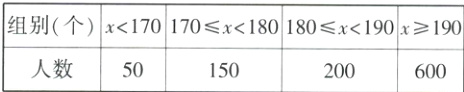
答案： 答案 $\frac{4}{5}$
解析 由题意，得P(1分钟跳绳成绩为满分)=$\frac{200 + 600}{1000}=\frac{4}{5}$.

11.一个密码锁的密码由三个数字组成,每个数字都是0至9这十个数字中的一个,只有当三个数字与所设定的密码相同时,才能将锁打开.粗心的小明忘了中间的数字,他一次就能打开该锁的概率是________.

答案： 答案 $\frac{1}{10}$
解析 密码由三个数字组成，中间的数字忘记了，则中间的数字可能是0~9中的一个，那么有10种等可能的结果，只有一种结果可以打开该锁，
所以他一次就能打开该锁的概率为$\frac{1}{10}$.

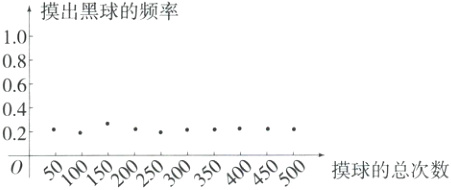
12.社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里,装有20个除颜色不同外其余均相同的黑、白两种球.将盒子里面的球搅匀后,从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象,如图所示,经分析可以推断“摸出黑球”的概率为________.

答案： 答案 0.2
解析 由题图可知，随着摸球次数的增加，摸出黑球的频率逐渐稳定在0.2左右，所以估计“摸出黑球”的概率为0.2.

13.(2023山东聊城中考)在一个不透明的袋子中,装有五个分别标有数$-\sqrt{3},\sqrt{6},0,2,\pi$的小球,这些小球除数外其他完全相同.从袋子中随机摸出两个小球,两球上的数字之积恰好是有理数的概率为________.

答案：
答案 $\frac{2}{5}$
解析 根据题意画树状图如下:

共有20种等可能的结果，其中两球上的数之积恰好是有理数的结果有8种，
∴两球上的数之积恰好是有理数的概率为$\frac{8}{20}=\frac{2}{5}$.

14.甲、乙两人玩猜数字游戏,游戏规则:有四个数字0、1、2、3,先由甲任选一个数字,记为m,再由乙猜甲刚才所选的数字,记为n(n为0,1,2,3中的一个数字),若m、n满足$|m - n|\leq1$,则甲、乙两人“心有灵犀”,则甲、乙两人“心有灵犀”的概率是________.

答案：
答案 $\frac{5}{8}$
解析 画树状图如下:

共有16种等可能的结果，其中m、n满足|m - n|≤1的结果有10种，
∴甲、乙两人“心有灵犀”的概率为$\frac{10}{16}=\frac{5}{8}$.

三、解答题(本大题共4小题,共44分)
15.(2024浙江杭州下城三模)(10分)某停车场,现仅剩下“C001”“C002”“C003”“C004”四个车位.
(1)若有一辆小汽车停车,则这辆车停在“C002”号车位的概率是________;
(2)分别记这四个车位为A、B、C、D,小明和小红同时来到该处停车,用画树状图或列表的方法,求两人把车停在相邻车位的概率.

答案：
解析
(1)
∵现仅剩下“C001”“C002”“C003”“C004”四个车位，
∴这辆小汽车停在“C002”号车位的概率是$\frac{1}{4}$.
(2)画树状图如下：

共有12种等可能的结果，其中小明和小红两人把车停在相邻车位的结果有6种，
∴两人把车停在相邻车位的概率为$\frac{6}{12}=\frac{1}{2}$.

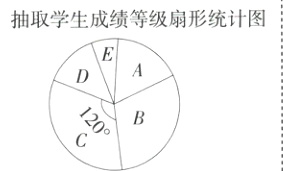
16.(2024四川广元中考)(10分)广元市开展“蜀道少年”选拔活动,旨在让更多的青少年关注蜀道、了解蜀道、热爱蜀道、宣传蜀道,进一步挖掘和传承古蜀道文化、普及蜀道知识,为此某校开展了“蜀道文化知识竞赛”活动,并从全校学生中抽取了若干学生的竞赛成绩进行整理、描述和分析(竞赛成绩用x表示,总分为100分,共分成五个等级,A:$90\leq x\leq100$;B:$80\leq x＜90$;C:$70\leq x＜80$;D:$60\leq x＜70$;E:$50\leq x＜60$),并绘制了尚不完整的统计图和统计表.
抽取学生成绩等级人数统计表

扇形图中C等级区域所对应的扇形圆心角的度数是120°.
(1)样本容量为________,m = ________;
(2)全校1 200名学生中,请估计A等级的学生人数;
(3)全校有5名学生得满分,七年级1人,八年级2人,九年级2人,从这5名学生中任意选择两人在国旗下分享自己与蜀道的故事,请你用画树状图或列表的方法,求这两人来自同一个年级的概率.

答案：
解析
(1)样本容量为$30\div\frac{120^{\circ}}{360^{\circ}} = 90$，
∴m = 90 - 27 - 30 - 12 - 6 = 15.
(2)$1200\times\frac{15}{90}=200$(名).
答：全校1200名学生中，估计A等级的学生人数为200.
(3)把七年级的1人记为A，八年级的2人分别记为B、C，九年级的2人分别记为D、E，
画树状图如下：

共有20种等可能的结果，其中选择的两人来自同一个年级的结果有4种，
∴这两人来自同一个年级的概率=$\frac{4}{20}=\frac{1}{5}$.