《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

7.(2023四川乐山中考)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”，如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25，小正方形面积为1，则sinθ = (　　)
　　　　　　　
A.$\frac{4}{5}$　　
　B.$\frac{3}{5}$　　
　C.4　　
　D.$\frac{1}{5}$

答案： 7A设大正方形的边长为c,直角三角形较短的直角边长为a,较长的直角边长为b,由题意可得$c^{2}=25$,$b - a=\sqrt{1}=1$,$a^{2}+b^{2}=c^{2}$,解得a = 3,b = 4,c = 5,
∴$\sin\theta=\frac{b}{c}=\frac{4}{5}$,故选A.

8.(2024福建福州鼓楼期末)古希腊数学家丢番图在《算术》中提到了一元二次方程的问题，欧几里得的《原本》中记载了形如$x^{2}+bx = m^{2}(b＞0,m＞0)$的方程的图解法：如图，画Rt△ABC，使∠ACB = 90°，$BC=\frac{b}{2}$，$AC = m$，再在斜边AB上截取$BD=\frac{b}{2}$，则该方程的一个正实数根等于(　　)
　　　　　　　　　　　　　　
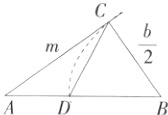
A.AD的长　　　　　
　B.AC的长
C.BC的长　　　　　
　D.CD的长

答案： 8A
∵$\angle ACB = 90^{\circ}$,$BC=\frac{b}{2}$,$AC = m$,
∴$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{m^{2}+(\frac{b}{2})^{2}}=\sqrt{m^{2}+\frac{b^{2}}{4}}$,
∴$AD = AB - BD=\sqrt{m^{2}+\frac{b^{2}}{4}}-\frac{b}{2}=\frac{\sqrt{4m^{2}+b^{2}}-b}{2}$,
∵$x^{2}+bx = m^{2}(b ＞ 0,m ＞ 0)$用求根公式求得$x=\frac{-b\pm\sqrt{b^{2}+4m^{2}}}{2}$,
∴$x_{1}=\frac{\sqrt{4m^{2}+b^{2}}-b}{2}$,$x_{2}=\frac{-\sqrt{4m^{2}+b^{2}}-b}{2}$,
∴AD的长就是方程的一个正实数根,故选A.

9.(2023江西中考)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺（即图中的ABC）.“偃矩以望高”的意思是把“矩”仰立放，可测量物体的高度.如图，点A，B，Q在同一水平线上，∠ABC和∠AQP均为直角，AP与BC相交于点D.测得$AB = 40$cm，$BD = 20$cm，$AQ = 12$m，则树高$PQ=$________m.
　　　　　

答案： 9答案6
解析
∵$\angle ABC=\angle AQP = 90^{\circ}$,
∴BC//PQ,
∴$\triangle ABD\sim\triangle AQP$,
∴$\frac{AB}{BD}=\frac{AQ}{QP}$,
∵AB = 40 cm = 0.4 m,BD = 20 cm = 0.2 m,AQ = 12 m,
∴$\frac{0.4}{0.2}=\frac{12}{QP}$,
∴QP = 6 m,
∴树高PQ = 6 m.

10.《海岛算经》第一个问题的大意是：如图，要测量海岛上一座山峰A的高度AH，立两根高3丈的标杆BC和DE，两杆之间的距离$BD = 1000$步，D、B、H成一线，从B处退行123步到F，从F观察A点，A、C、F三点成一线；从D处退行127步到G，从G观察A点，A、E、G三点也成一线.试计算山峰的高度AH及HB的长（这里1步 = 6尺，1丈 = 10尺，结果用丈表示）.
　　　　　　　

答案： 10解析由题意得DE//AH//BC,
∴$\triangle DEG\sim\triangle HAG$,$\triangle BCF\sim\triangle HAF$,
∴$\frac{DG}{HG}=\frac{DE}{AH}$,$\frac{BF}{HF}=\frac{BC}{AH}$,又
∵BC = DE,
∴$\frac{BF}{HF}=\frac{DG}{HG}$,
即$\frac{123}{123 + HB}=\frac{127}{127 + 1000 + HB}$,
∴BH = 30750(步),30750步 = 18450丈,
∴BH = 18450丈.
又
∵$\frac{BF}{HF}=\frac{BC}{AH}$,
∴$AH=\frac{BC\cdot HF}{BF}=\frac{(3×10)\div6×(30750 + 123)}{123}=1255$(步),1255步 = 753丈.
∴AH = 753丈.