《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

17.应用意识 (2024北京石景山期末)2024年3月14日是第五个“国际数学日”,也叫“π日”.为了营造良好的数学学习氛围,弘扬数学文化,传承数学精神.某校决定购买A ,B两种数学类图书共50本.若购买9本A种图书和6本B种图书共需390元;若购买5本A种图书和8本B种图书共需310元.
(1)A,B两种图书的单价分别为多少元?
(2)若学校决定购买A种图书比B种图书的数量至少多5本,又不超过B种的2倍,怎样购买才能使费用最少?并求出最少费用.

答案： 解析
(1)设A种图书每本x元，B种图书每本y元，
由题意可列方程组$\begin{cases}5x + 8y = 310\\9x + 6y = 390\end{cases}$，解得$\begin{cases}x = 30\\y = 20\end{cases}$.
答：A种图书每本30元，B种图书每本20元.
(2)设该校购买A种图书m本，则购买B种图书(50 - m)本，
由题意得$\begin{cases}m-(50 - m)≥5\\m≤2(50 - m)\end{cases}$，
解得$\frac{55}{2}≤m≤\frac{100}{3}$，且m为正整数，
∵A种图书单价高，
∴购买A种图书越少越省钱，
∴m取最小值28时，总费用最少，
最少费用为28×30+(50 - 28)×20 = 1280(元).
答：购买A种图书28本，购买B种图书22本时，总费用最少，为1280元.

18.应用意识 (2024北京石景山校级模拟)某公园内人工湖上有一座拱桥(横截面如图所示),跨度AB为4米.在距点A水平距离为d米的地点,拱桥距离水面的高度为h米.小红根据学习函数的经验,对d和h之间的关系进行了探究.(M9226002)

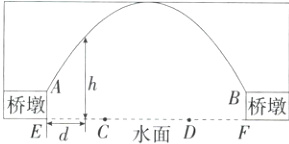
(1)经过测量,得出了d和h的几组对应值,如下表.
|d/米|0|0.6|1|1.8|2.4|3|3.6|4|
|----|----|----|----|----|----|----|----|----|
|h/米|0.88|1.90|2.38|2.86|2.80|2.38|1.60|0.88|
在d和h这两个变量中,______是自变量,______是这个变量的函数.
(2)在平面直角坐标系xOy中,画出表格中数据所确定的函数图象.

(3)结合表格数据和函数图象,解决问题:
①桥墩露出水面的高度AE为______米.
②公园欲开设游船项目,现有长为3.5米,宽为1.5米,露出水面高度为2米的游船.为安全起见,公园要在水面上的C,D两处设置警戒线,并且CE = DF,要求游船能从C,D两点之间安全通过,则C处距桥墩的距离CE至少为______米.(精确到0.1米)

答案：
解析
(1)d是自变量，h是这个变量的函数.
(2)如图.

(3)①当d = 0时，h = 0.88，
∴桥墩露出水面的高度AE为0.88米.
②设二次函数的解析式为$h = ad^{2}+bd + c$，
把(0，0.88)、(1，2.38)、(3，2.38)代入得$\begin{cases}c = 0.88\\a + b + c = 2.38\\9a + 3b + c = 2.38\end{cases}$，解得$\begin{cases}a = - 0.5\\b = 2\\c = 0.88\end{cases}$，
∴$h = - 0.5d^{2}+2d + 0.88$，对称轴为直线d = 2.
令h = 2，得$2 = - 0.5d^{2}+2d + 0.88$，
解得$d≈3.3$(舍去)或$d≈0.7$.
∴C处距桥墩的距离CE至少为0.7米.