《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

8. [鸡爪模型]（2023北京八中月考）如图，P为正方形ABCD内一点，且BP = 2，PC = 3，∠APB = 135°，将△APB绕点B顺时针旋转90°得到△CP'B，连接PP'，求AP的长.（M9223003）

答案： 解析
∵△CP'B是由△APB旋转得到的，
∴∠APB = ∠CP'B = 135°，∠ABP = ∠CBP'，BP = BP'，AP = CP'，
∵∠ABP + ∠PBC = 90°，
∴∠CBP' + ∠PBC = 90°，即∠PBP' = 90°，
∴△BPP'是等腰直角三角形，
∴∠BP'P = 45°，PP' = $\sqrt{BP^{2}+BP'^{2}}$ = 2$\sqrt{2}$，
∵∠CP'B = 135°，
∴∠PP'C = 90°，
∵PC = 3，
∴CP' = $\sqrt{PC^{2}-PP'^{2}}$ = $\sqrt{9 - 8}$ = 1，
∴AP = CP' = 1.
方法解读
本题中由BP，BA，BC组成的“鸡爪模型”较为特殊，此模型有两条“等爪”，即BA = BC，且这两条等爪的夹角是特殊角(90°).对“鸡爪模型”中的△APB旋转，得到△CP'B，故AP = CP'，根据旋转的性质可知△BPP'是等腰直角三角形，求出PP'的长度，在Rt△CPP'中利用勾股定理即可求得CP'的长，从而得解.

9.（2024北京丰台期末）如图，△ABC绕某点按一定方向旋转一定角度后得到△A₁B₁C₁，点A，B，C分别对应点A₁，B₁，C₁.
（1）在图中画出△A₁B₁C₁；
（2）△A₁B₁C₁是以点_______（填“O₁”“O₂”或“O₃”）为旋转中心，将△ABC_______时针旋转_______度得到的.

答案：
解析
(1)如图，△A₁B₁C₁即为所求.

(2)△A₁B₁C₁是以点O₁为旋转中心，将△ABC顺时针旋转90度得到的.

10. 如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）.
（1）以点B为旋转中心，将△ABC按逆时针方向旋转90°，得到△A₁BC₁，画出△A₁BC₁.
（2）用无刻度的直尺画图.（要求：保留关键作图痕迹，无需写作法）
①过点A作BC的垂线，交BC于点H，并标出点H；
②在AC上找一点P，使得CP = $\frac{2}{3}$AC，并标出点P.

答案：
解析
(1)如图所示，△A₁BC₁即为所求.

(2)①如图所示，取格点K，连接AK，交BC于点H，由网格特点可知AK⊥BC，则点H即为所求.
②如图所示，取AC与格线的交点P，点P即为所求.
易证明△CPQ∽△CAT，即可得到$\frac{CP}{CA}=\frac{CQ}{CT}=\frac{2}{3}$.

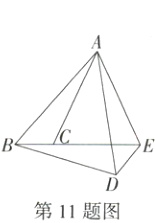
11.（2023天津中考，11，★★☆）如图，把△ABC以点A为中心逆时针旋转得到△ADE，点B，C的对应点分别是点D，E，且点E在BC的延长线上，连接BD，则下列结论一定正确的是（M9223003） （ ）

A.∠CAE = ∠BED
B.AB = AE
C.∠ACE = ∠ADE
D.CE = BD

答案：
A 如图，设AD与BE的交点为O，
∵把△ABC以点A为中心逆时针旋转得到△ADE，
∴∠ABC = ∠ADE，∠BAD = ∠CAE，又
∵∠AOB = ∠DOE，
∴∠BED = ∠BAD = ∠CAE.故A中结论一定正确.

12. [最短距离问题]（2024北京师大实验华夏女子中学零模，8，★★☆）如图，在矩形ABCD中，AB = 6，BC = 6$\sqrt{3}$，点P在线段BC上运动（含B，C两点），连接AP，以点A为中心，将线段AP逆时针旋转60°到AQ，连接DQ，则线段DQ的最小值为（M9223003） （ ）

A.$\frac{5}{2}$
B.5$\sqrt{2}$
C.$\frac{5\sqrt{3}}{3}$
D.3

答案：
D 如图，以AB为边向右作等边△ABF，作射线FQ交AD于点E，过点D作DH⊥QE于H.由题意得△APQ为等边三角形，

∵四边形ABCD是矩形，
∴∠ABP = ∠BAD = 90°，
∵△ABF，△APQ都是等边三角形，
∴∠BAF = ∠PAQ = 60°，BA = FA，PA = QA，
∴∠BAP = ∠FAQ.在△BAP和△FAQ中，
$\begin{cases}BA = FA,\\\angle BAP = \angle FAQ,\\PA = QA,\end{cases}$
∴△BAP≌△FAQ，
∴∠AFQ = ∠ABP = 90°，
∴点Q在与过点F且与AF垂直的射线上运动，
∵∠FAE = 90° - 60° = 30°，
∴∠AEF = 90° - 30° = 60°.
∵AB = AF = 6，
∴AE = AF÷cos 30° = 4$\sqrt{3}$，
∵AD = BC = 6$\sqrt{3}$，
∴DE = AD - AE = 2$\sqrt{3}$，
∵DH⊥EF，∠DEH = ∠AEF = 60°，
∴DH = DE·sin 60° = 2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$ = 3.根据垂线段最短可知，当Q与H重合时，DQ的值最小，最小值为3.故选D.

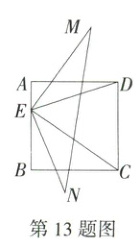
13.（2024北京师大附中一模，16，★★☆）如图，正方形ABCD的边长为2，点E是边AB上的动点，连接ED、EC，将ED绕点E顺时针旋转90°得到EN，将EC绕点E逆时针旋转90°得到EM，连接MN，则线段MN的取值范围为_______.

答案：
答案 4≤MN≤2$\sqrt{5}$
解析 如图，过点M作MF⊥AB，交BA的延长线于点F，过点N作NG⊥AB，交AB的延长线于点G，作NH⊥FM于点H，则∠EFM = ∠EGN = ∠FHN = ∠NHM = 90°，

由旋转的性质得EM = EC，EN = ED，∠CEM = ∠DEN = 90°，
∴∠MEF + ∠CEB = 90°，∠DEA + ∠NEG = 90°，
∵∠EFM = ∠DAE = 90°，
∴∠MEF + ∠EMF = 90°，∠DEA + ∠EDA = 90°，
∴∠CEB = ∠EMF，∠NEG = ∠EDA，由题意得AB = AD = BC = 2，设AE = x(0≤x≤2)，则BE = 2 - x.
在△MEF和△ECB中，
$\begin{cases}\angle EFM = \angle CBE = 90^{\circ},\\\angle EMF = \angle CEB,\\EM = EC,\end{cases}$
∴△MEF≌△ECB，
∴MF = BE = 2 - x，EF = BC = 2，
同理NG = AE = x，EG = AD = 2，
∴FG = EF + EG = 2 + 2 = 4.
∵∠MFE = ∠NGE = ∠FHN = 90°，
∴四边形FGNH是矩形，
∴HN = FG = 4，FH = NG = x，
∴MH = MF - FH = 2 - x - x = 2 - 2x，在Rt△MNH中，MN² = MH² + HN² = (2 - 2x)² + 4² = 4(x - 1)² + 16，
∵0≤x≤2，
∴0≤(x - 1)²≤1，
∴16≤4(x - 1)² + 16≤20，即16≤MN²≤20，
∵MN＞0，
∴线段MN的取值范围为4≤MN≤2$\sqrt{5}$.