第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
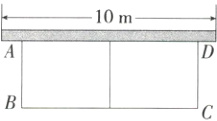
19.易错题(14分)如图,一面利用墙(墙的最大可用长度为10m),用长为24m的篱笆围成中间隔有一道篱笆的矩形花圃.设花圃的宽AB为x(m),面积为y(m²).
(1)写出y与x之间的函数关系式及自变量x的取值范围.
(2)围成花圃的最大面积是多少?这时花圃的宽等于多少?(M9226003)
(1)写出y与x之间的函数关系式及自变量x的取值范围.
(2)围成花圃的最大面积是多少?这时花圃的宽等于多少?(M9226003)

答案:
解析
(1)花圃的宽 $AB$ 为 $x$ m,则花圃的长 $BC$ 为 $(24 - 3x)$ m,
∴ $y = x(24 - 3x)=-3x^{2}+24x$.
∵ 墙的最大可用长度为 10 m,
∴ $24 - 3x\leqslant10$,
∴ $x\geqslant\frac{14}{3}$,
∵ 篱笆长为 24 m,
∴ $3x<24$,
∴ $x<8$,
∴ $\frac{14}{3}\leqslant x<8$.
综上,$y$ 与 $x$ 之间的函数关系式为 $y = -3x^{2}+24x$,自变量 $x$ 的取值范围是 $\frac{14}{3}\leqslant x<8$.
(2)
∵ $y = -3x^{2}+24x=-3(x - 4)^{2}+48$,
∴ 抛物线的对称轴为直线 $x = 4$,抛物线开口向下,
∴ 在对称轴右侧,$y$ 随 $x$ 的增大而减小.
∵ $\frac{14}{3}\leqslant x<8$,且 $4<\frac{14}{3}$,
∴ 当 $x = \frac{14}{3}$ 时,$y_{max}=-3(\frac{14}{3}-4)^{2}+48$
$=-3×\frac{4}{9}+48 = 46\frac{2}{3}$.
∴ 围成花圃的最大面积是 $46\frac{2}{3}$ $m^{2}$,这时花圃的宽等于 $\frac{14}{3}$ m.
易错警示
本题的易错点在于求最值时,忽视自变量的取值范围,易计算成当 $x = 4$ 时取得最大值.
(1)花圃的宽 $AB$ 为 $x$ m,则花圃的长 $BC$ 为 $(24 - 3x)$ m,
∴ $y = x(24 - 3x)=-3x^{2}+24x$.
∵ 墙的最大可用长度为 10 m,
∴ $24 - 3x\leqslant10$,
∴ $x\geqslant\frac{14}{3}$,
∵ 篱笆长为 24 m,
∴ $3x<24$,
∴ $x<8$,
∴ $\frac{14}{3}\leqslant x<8$.
综上,$y$ 与 $x$ 之间的函数关系式为 $y = -3x^{2}+24x$,自变量 $x$ 的取值范围是 $\frac{14}{3}\leqslant x<8$.
(2)
∵ $y = -3x^{2}+24x=-3(x - 4)^{2}+48$,
∴ 抛物线的对称轴为直线 $x = 4$,抛物线开口向下,
∴ 在对称轴右侧,$y$ 随 $x$ 的增大而减小.
∵ $\frac{14}{3}\leqslant x<8$,且 $4<\frac{14}{3}$,
∴ 当 $x = \frac{14}{3}$ 时,$y_{max}=-3(\frac{14}{3}-4)^{2}+48$
$=-3×\frac{4}{9}+48 = 46\frac{2}{3}$.
∴ 围成花圃的最大面积是 $46\frac{2}{3}$ $m^{2}$,这时花圃的宽等于 $\frac{14}{3}$ m.
易错警示
本题的易错点在于求最值时,忽视自变量的取值范围,易计算成当 $x = 4$ 时取得最大值.
20.(2024北京北大附中零模)(14分)某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,水柱从喷水头喷出到落于湖面的路径形状可以看成抛物线的一部分.若记水柱上某一位置与水管的水平距离为d米,与湖面的垂直高度为h米.下表记录了d与h的五组数据:
|d(米)|0|1|2|3|4|
|--|--|--|--|--|--|
|h(米)|0.5|1.25|1.5|1.25|0.5|
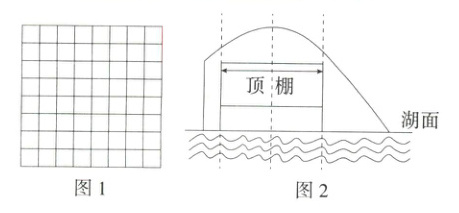
根据上述信息,解决以下问题:
(1)在网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示h与d函数关系的图象.
(2)若水柱最高点距离湖面的高度为m米,则m = ________.
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从水柱下方通过.如图2所示,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米.已知游船顶棚的宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数)
|d(米)|0|1|2|3|4|
|--|--|--|--|--|--|
|h(米)|0.5|1.25|1.5|1.25|0.5|

根据上述信息,解决以下问题:
(1)在网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示h与d函数关系的图象.
(2)若水柱最高点距离湖面的高度为m米,则m = ________.
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从水柱下方通过.如图2所示,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米.已知游船顶棚的宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数)
答案:
解析
(1)以水管与湖面的交点为原点,水管所在的直线为纵轴建立平面直角坐标系,如图所示:
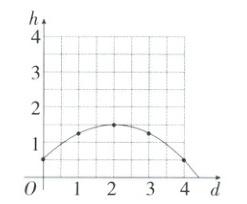
(2)根据题意可知,该抛物线的对称轴为 $x = 2$,此时水柱最高,即 $m = 1.5$.
(3)根据图象可设二次函数的解析式为 $h = a(d - 2)^{2}+1.5$,
将 $(0,0.5)$ 代入 $h = a(d - 2)^{2}+1.5$,得 $a = -\frac{1}{4}$,
∴ 抛物线的解析式为 $h = -\frac{1}{4}d^{2}+d + 0.5$.
设调节后抛物线的解析式为 $h = -\frac{1}{4}d^{2}+d + 0.5 + m$,
由题意可知,当横坐标为 $2+\frac{3}{2}=\frac{7}{2}$ 时,纵坐标的值大于 $2 + 0.5 = 2.5$,
∴ $-\frac{1}{4}×(\frac{7}{2})^{2}+\frac{7}{2}+0.5 + m\geqslant2.5$,解得 $m\geqslant\frac{25}{16}$,
∴ 水管高度至少向上调节 $\frac{25}{16}$ 米,
∵ $0.5+\frac{25}{16}\approx2.1$(米),
∴ 公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到 2.1 米才能符合要求.
解析
(1)以水管与湖面的交点为原点,水管所在的直线为纵轴建立平面直角坐标系,如图所示:

(2)根据题意可知,该抛物线的对称轴为 $x = 2$,此时水柱最高,即 $m = 1.5$.
(3)根据图象可设二次函数的解析式为 $h = a(d - 2)^{2}+1.5$,
将 $(0,0.5)$ 代入 $h = a(d - 2)^{2}+1.5$,得 $a = -\frac{1}{4}$,
∴ 抛物线的解析式为 $h = -\frac{1}{4}d^{2}+d + 0.5$.
设调节后抛物线的解析式为 $h = -\frac{1}{4}d^{2}+d + 0.5 + m$,
由题意可知,当横坐标为 $2+\frac{3}{2}=\frac{7}{2}$ 时,纵坐标的值大于 $2 + 0.5 = 2.5$,
∴ $-\frac{1}{4}×(\frac{7}{2})^{2}+\frac{7}{2}+0.5 + m\geqslant2.5$,解得 $m\geqslant\frac{25}{16}$,
∴ 水管高度至少向上调节 $\frac{25}{16}$ 米,
∵ $0.5+\frac{25}{16}\approx2.1$(米),
∴ 公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到 2.1 米才能符合要求.
查看更多完整答案,请扫码查看


