《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

14.(将军饮马模型)(2023北京海淀清华附中月考,7,★☆☆)如图,直线l,m相交于点O,P为两直线外一点,且OP = 2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是(M9223004)(　　　)

A.5
B.6
C.7
D.8

答案：
14A 如图，连接OP₁，PP₁，OP₂，PP₂，P₁P₂，
　　　　　　　
∵ P₁是P关于直线l的对称点，
∴ 直线l是线段PP₁的垂直平分线，
∴ OP₁=OP=2.8，
∵ P₂是P关于直线m的对称点，
∴ 直线m是线段PP₂的垂直平分线，
∴ OP₂=OP=2.8，当P₁，O，P₂不在同一条直线上时，OP₁ - OP₂＜P₁P₂＜OP₁ + OP₂，即0＜P₁P₂＜5.6，当P₁，O，P₂在同一条直线上时，P₁P₂=OP₁ + OP₂=5.6，
∴ P₁，P₂之间的距离可能是5，故选A.
·方法解读
本题属于将军饮马模型中的一点两线型问题，需构造一定点关于两定直线的对称点，连接对称点，利用“两点之间，线段最短”解决问题.

15.(2024甘肃中考,14,★☆☆)围棋起源于中国,古代称为“弈”.如图所示的是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点______的位置,则所得的对弈图是轴对称图形.(填写A,B,C,D中的一处即可,A,B,C,D位于棋盘的格点上)

答案： 答案 A(答案不唯一)
解析 白方如果落子于点A的位置，则所得的对弈图是轴对称图形.(答案不唯一)

16.(将军饮马模型)(2024四川成都中考,13,★☆☆)如图,在平面直角坐标系xOy中,已知A(3,0),B(0,2),过点B作y轴的垂线l,P为直线l上一动点,连接PO,PA,则PO + PA的最小值为______.

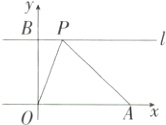
答案： 答案 5
解析 作点O关于直线l的对称点O′(图略)，
∵ l⊥y轴，B(0，2)，
∴ O′(0，4)，连接AO′，AO′与直线l的交点为点P，此时PO+PA取最小值，最小值为AO′的长，根据勾股定理可得AO′=$\sqrt{3^{2}+4^{2}}$=5.

17.(跨物理·反弹)(2022北京丰台期中,16,★☆☆)如图,弹性小球从点P(0,1)出发,沿图中所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹前后的轨迹线与边的夹角相等,当小球第1次碰到正方形的边时的点为P1(2,0),第2次碰到正方形的边时的点为P2(4,1),……,第n次碰到正方形的边时的点为Pn,则点P2021的坐标为__________.(M9223005)

答案：
答案 (4，3)
解析 如图：
　　　　　　
由图可知小球从P₂反弹后到P₃(0，3)，再反弹到P₄(2，4)，再反弹到P₅(4，3)，再反弹到点P(0，1)之后，循环反弹，每6次为一个循环，
∵ 2021÷6=336……5，
∴ 点P₂₀₂₁的坐标是(4，3).

18.(分类讨论思想)(2024北京北师大附属实验中学二模,13,★☆☆)如图,在长方形ABCD中,AD = 5,AB = 8,点E为射线DC上一个动点,把△ADE沿直线AE折叠.当点D的对应点F刚好落在线段AB的垂直平分线上时,DE的长为______.

答案：
答案 $\frac{5}{2}$或10
解析 设线段AB的垂直平分线为MN.
分两种情况：①如图1，当点F在矩形内部时，
∵ 点F在AB的垂直平分线MN上，
∴ AN=4.
∵ AF=AD=5，
∴ 由勾股定理得FN=3，
∴ FM=2，设DE=y，则EM=4 - y，FE=y.在△EMF中，由勾股定理得y²=(4 - y)²+2²，
∴ y=$\frac{5}{2}$，即DE的长为$\frac{5}{2}$.
②如图2，当点F在矩形外部时，同①的方法可得FN=3，
∴ FM=8，设DE=z，则EM=z - 4，FE=z，在△EMF中，由勾股定理得z²=(z - 4)²+8²，
∴ z=10，即DE的长为10.
综上所述，点F刚好落在线段AB的垂直平分线上时，DE的长为$\frac{5}{2}$或10.

19.(2023北京汇文中学期中,27,★☆☆)如图,在平面直角坐标系xOy中,直线l为第一、三象限的角平分线,点P关于y轴的对称点称为P的一次反射点,记作P1;P1关于直线l的对称点为点P的二次反射点,记作P2.例如,点(-2,5)的一次反射点为(2,5),二次反射点为(5,2).根据定义,回答下列问题:(M9223005)
(1)点(3,4)的一次反射点为______,二次反射点为______;
(2)当点A在第三象限时,点M(-4,1),N(3,-1),Q(-1,-5)中可能是点A的二次反射点的是______;
(3)若点A在第二象限,点A1,A2分别是点A的一次、二次反射点,∠A1OA2 = 50°,求射线OA与x轴所夹锐角的度数;
(4)若点A在y轴左侧,点A1,A2分别是点A的一次、二次反射点,△AA1A2是等腰直角三角形,请直接写出点A在平面直角坐标系xOy中的位置.

答案：
解析 （1）(-3，4)；(4，-3).
（2）M.详解：
∵点A在第三象限，
∴ 一次反射点在第四象限，二次反射点在第二象限，
∴ 点M(-4，1)，N(3，-1)，Q(-1，-5)中可能是点A的二次反射点的是M(-4，1).
（3）如图：
　　　　　　
∵ ∠A₁OA₂=50°，
∴ OA₁与x轴所夹锐角的度数为20°或70°.
根据对称性可知，射线OA与x轴所夹锐角的度数为20°或70°.
（4）点A在x轴负半轴上或在y轴左侧且在直线y=x上.
详解：①如图，观察图象可知，当点A在x轴负半轴上时，△AA₁A₂是等腰直角三角形.
　　　　　　　
②如图，观察图象可知，当点A在y轴左侧且在直线y=x上时，△AA₁A₂是等腰直角三角形.
　　　　　　　
综上所述，点A在x轴负半轴上或在y轴左侧且在直线y=x上.