第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
5.(2024北京海淀一模)在平面直角坐标系xOy中,对于图形M与图形N给出如下定义:P为图形N上任意一点,将图形M绕点P顺时针旋转90°得到M',将所有M'组成的图形记作M'',称M''是图形M关于图形N的“关联图形”.
(1)已知A(−2,0),B(2,0),C(2,t),其中t≠0.
①若t = 1,请在图中画出点A关于线段BC的“关联图形”;
②若点A关于线段BC的“关联图形”与坐标轴有公共点,直接写出t的取值范围.
(2)对于平面上一条长度为a的线段和一个半径为r的圆,点S在线段关于圆的“关联图形”上,记点S的纵坐标的最大值和最小值的差为d,当这条线段和圆的位置变化时,直接写出d的取值范围(用含a和r的式子表示).
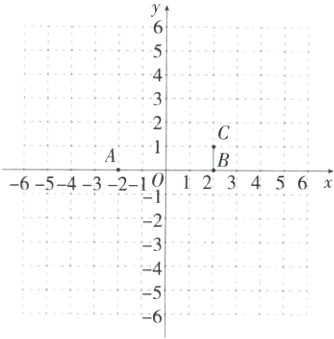
(1)已知A(−2,0),B(2,0),C(2,t),其中t≠0.
①若t = 1,请在图中画出点A关于线段BC的“关联图形”;
②若点A关于线段BC的“关联图形”与坐标轴有公共点,直接写出t的取值范围.
(2)对于平面上一条长度为a的线段和一个半径为r的圆,点S在线段关于圆的“关联图形”上,记点S的纵坐标的最大值和最小值的差为d,当这条线段和圆的位置变化时,直接写出d的取值范围(用含a和r的式子表示).

答案:
解析
(1)①如图,线段B'C'即为所求.

②t≤-4或t≥2.
(2)画出分析图,如图所示,线段AB的长度为a,圆N的半径为r,点A、B分别绕点N顺时针旋转90°得到N1,N2,

分析可知△BNP∽△BN1Q且相似比为1:$\sqrt{2}$,
可得圆N1,N2的半径均为$\sqrt{2}$r,
∴2$\sqrt{2}$r≤d≤2$\sqrt{2}$r+a.
解析
(1)①如图,线段B'C'即为所求.

②t≤-4或t≥2.
(2)画出分析图,如图所示,线段AB的长度为a,圆N的半径为r,点A、B分别绕点N顺时针旋转90°得到N1,N2,

分析可知△BNP∽△BN1Q且相似比为1:$\sqrt{2}$,
可得圆N1,N2的半径均为$\sqrt{2}$r,
∴2$\sqrt{2}$r≤d≤2$\sqrt{2}$r+a.
6.(2023北京门头沟二模)在平面直角坐标系xOy中,线段AB = 4,点M,N在线段AB上,且MN = 2,P为MN的中点,如果任取一点Q,将点Q绕点P顺时针旋转180°得到点Q',则称点Q'为点Q关于线段AB的“旋平点”.
(1)如图1,已知A(−1,0),B(3,0),Q(1,2),如果Q'(a,b)为点Q关于线段AB的“旋平点”,画出示意图,写出a的取值范围;
(2)如图2,⊙O的半径为3,点A,B在⊙O上,点Q(1,0),如果在直线x = m上存在点Q关于线段AB的“旋平点”,求m的取值范围.
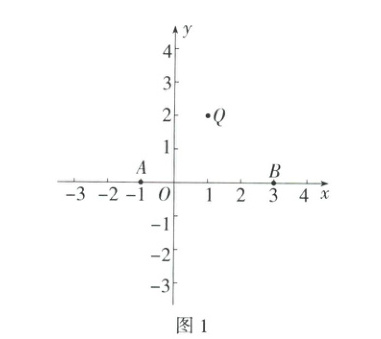

(1)如图1,已知A(−1,0),B(3,0),Q(1,2),如果Q'(a,b)为点Q关于线段AB的“旋平点”,画出示意图,写出a的取值范围;
(2)如图2,⊙O的半径为3,点A,B在⊙O上,点Q(1,0),如果在直线x = m上存在点Q关于线段AB的“旋平点”,求m的取值范围.


答案:
解析
(1)如图,当线段MN一端与A重合时,中点P与O重合,连接OQ,将点Q绕点O顺时针旋转180°得到点Q1,
由中心对称得点Q1的坐标为(-1,-2);
当线段MN一端与B重合时,中点P的坐标为(2,0),
连接PQ,将点Q绕点P顺时针旋转180°得到点Q2,
由中心对称得点Q2的坐标为(3,-2),
∴-1≤a≤3.

(2)
∵点Q在x轴上,
∴当点P也在x轴上时,点Q'的横坐标有最值,当点P在x轴上时,连接OM,则OM⊥AB,
∴BM=AM=$\frac{1}{2}$×4=2,
∵☉O的半径为3,
∴OM=$\sqrt{3^{2}-2^{2}}=\sqrt{5}$,
∵PM=1,
∴OP=$\sqrt{(\sqrt{5})^{2}+1^{2}}=\sqrt{6}$.
如图1,当点P在x轴负半轴上时,PQ=$\sqrt{6}$+1,

∴QQ'=2PQ=2$\sqrt{6}$+2,
∵1-(2$\sqrt{6}$+2)=-2$\sqrt{6}$-1,
∴Q'(-2$\sqrt{6}$-1,0);
如图2,当点P在x轴正半轴上时,PQ=$\sqrt{6}$-1,

∴QQ'=2PQ=2$\sqrt{6}$-2,
∵1+(2$\sqrt{6}$-2)=2$\sqrt{6}$-1,
∴Q'(2$\sqrt{6}$-1,0),
∴-2$\sqrt{6}$-1≤m≤2$\sqrt{6}$-1.
解析
(1)如图,当线段MN一端与A重合时,中点P与O重合,连接OQ,将点Q绕点O顺时针旋转180°得到点Q1,
由中心对称得点Q1的坐标为(-1,-2);
当线段MN一端与B重合时,中点P的坐标为(2,0),
连接PQ,将点Q绕点P顺时针旋转180°得到点Q2,
由中心对称得点Q2的坐标为(3,-2),
∴-1≤a≤3.

(2)
∵点Q在x轴上,
∴当点P也在x轴上时,点Q'的横坐标有最值,当点P在x轴上时,连接OM,则OM⊥AB,
∴BM=AM=$\frac{1}{2}$×4=2,
∵☉O的半径为3,
∴OM=$\sqrt{3^{2}-2^{2}}=\sqrt{5}$,
∵PM=1,
∴OP=$\sqrt{(\sqrt{5})^{2}+1^{2}}=\sqrt{6}$.
如图1,当点P在x轴负半轴上时,PQ=$\sqrt{6}$+1,

∴QQ'=2PQ=2$\sqrt{6}$+2,
∵1-(2$\sqrt{6}$+2)=-2$\sqrt{6}$-1,
∴Q'(-2$\sqrt{6}$-1,0);
如图2,当点P在x轴正半轴上时,PQ=$\sqrt{6}$-1,

∴QQ'=2PQ=2$\sqrt{6}$-2,
∵1+(2$\sqrt{6}$-2)=2$\sqrt{6}$-1,
∴Q'(2$\sqrt{6}$-1,0),
∴-2$\sqrt{6}$-1≤m≤2$\sqrt{6}$-1.
查看更多完整答案,请扫码查看


