《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

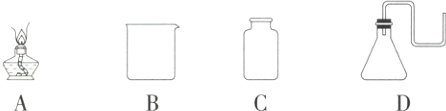
1.(跨化学·实验仪器)(2024重庆中考A卷)下列四种化学仪器的示意图中,是轴对称图形的是(　　　)

答案： 1C 直接根据轴对称图形的概念判断.只有C选项中的图形能找到这样的一条直线，使图形沿这条直线折叠，直线两旁的部分能够互相重合，选项A、B、D 均不行,故选C.

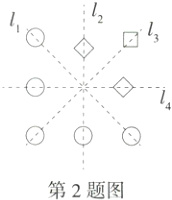
2.(2024北京通州一模)如图,由5个“〇”和3个“□”组成的图形关于某条直线对称,则该直线是(M9223004)(　　　)

A.l1
B.l2
C.l3
D.l4

答案： 2C 由题图可知,该图形关于直线l₃对称.故选C.

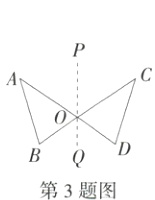
3.(2024河北中考)如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是点C,D.下列不一定正确的是(　　　)

A.AD⊥BC
B.AC⊥PQ
C.△ABO≌△CDO
D.AC//BD

答案：
3A 如图,连接AC、BD,
　　　　　　　　
∵ △ABO和△CDO关于直线PQ对称，
∴ △ABO≌△CDO，PQ⊥AC，PQ⊥BD（B、C选项正确），
∴ AC//BD，故D选项正确，
AD不一定垂直于BC，故A选项不一定正确，故选A.

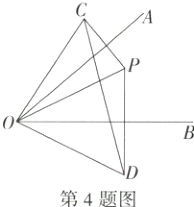
4.(2023北京海淀期中)如图,∠AOB = 40°,点P为∠AOB内一点,分别作P点关于直线OA,OB的对称点C,D,连接OP,OC,OD,CD.(M9223004)
则(1)∠CPD的度数是________;
(2)∠OCD的度数是________.

答案： 答案 （1）140° （2）50°
解析 （1）
∵点P，C关于直线OA对称，
∴ OP=OC，∠COA=∠POA=$\frac{1}{2}$∠COP，
∴ ∠OCP=∠OPC=$\frac{180° - ∠COP}{2}=\frac{180° - 2∠AOP}{2}$，
同理可知OP=OD，∠POB=∠DOB=$\frac{1}{2}$∠POD，
∴ ∠OPD=∠ODP=$\frac{180° - ∠POD}{2}=\frac{180° - 2∠POB}{2}$，
∴ ∠CPD = ∠OPC + ∠OPD = $\frac{180° - 2∠AOP}{2}+\frac{180° - 2∠POB}{2}=\frac{360° - 2(∠AOP + ∠POB)}{2}=\frac{360° - 2×40°}{2}=140°$.
（2）
∵点P，C关于直线OA对称，点P，D关于直线OB对称，
∴ OP=OC，OP=OD，
∴ OC=OD，
∴ ∠OCD=∠ODC.
由（1）知，∠COD=∠COP+∠POD=2∠AOB=80°，
∴ ∠OCD=$\frac{180° - ∠COD}{2}=\frac{180° - 80°}{2}=50°$.

5.如图,阴影部分是由3个小正方形组成的一个图形,若在图中剩余的小正方形中涂灰一个小正方形,使整个阴影部分为轴对称图形,涂法有________种.(M9223004)

答案：
答案 4
解析 如图所示，要在题图中剩余的小正方形中涂灰一个小正方形，使整个阴影部分为轴对称图形，只需将1，2，3，4中的一个小正方形涂灰即可，共有4种涂法.
　　　　　　　　　

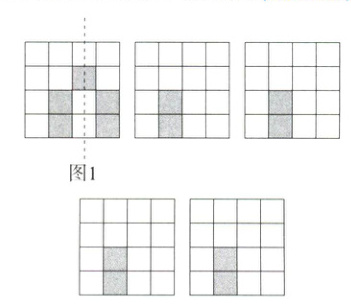
6.(2023北京通州期末)如图所示的是4×4的正方形网格,其中已有2个小方格涂成了阴影,现在要从其余14个白色小方格中选出3个也涂成阴影,使整个涂成阴影的图形为轴对称图形.请补全图形,并画出它们各自的对称轴(如图1),要求所画的四种方法不能重复.(M9223004)

答案：
解析 答案不唯一.如图所示:
　

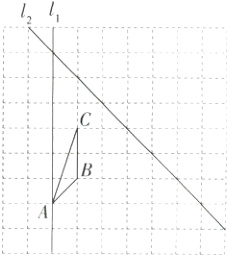
7.如图,在正方形网格中,给出了以格点(网格线的交点)为顶点的△ABC.(M9223004)
(1)画出△ABC关于直线l1对称的图形△A1B1C1;
(2)画出△ABC关于直线l2对称的图形△A2B2C2;
(3)△A1B1C1可由△A2B2C2绕点M顺时针旋转得到,在图中画出点M的位置.

答案：
解析 （1）如图，△A₁B₁C₁即为所求作.
（2）如图，△A₂B₂C₂即为所求作.
（3）点M的位置如图所示.