第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.(2024 北京东城一模)一个不透明的口袋中有三个完全相同的小球,把它们分别标号为 1,2,3. 随机摸出一个小球后放回,摇匀后再随机摸出一个小球,两次摸出的小球标号相同的概率为( )
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{6}$
D.$\frac{1}{9}$
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{6}$
D.$\frac{1}{9}$
答案:
B 列表如下:
| | 1 | 2 | 3 |
|----|----|----|----|
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
共有 9 种等可能的结果,其中两次摸出的小球标号相同的结果有 3 种,
∴ 两次摸出的小球标号相同的概率为$\frac{3}{9}=\frac{1}{3}$. 故选 B.
| | 1 | 2 | 3 |
|----|----|----|----|
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
共有 9 种等可能的结果,其中两次摸出的小球标号相同的结果有 3 种,
∴ 两次摸出的小球标号相同的概率为$\frac{3}{9}=\frac{1}{3}$. 故选 B.
2.(2024 河北中考)甲、乙、丙三张卡片正面分别写有$a + b$,$2a + b$,$a - b$,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当$a = 1$,$b = - 2$时,求取出的卡片上代数式的值为负数的概率.
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.
请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.

(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当$a = 1$,$b = - 2$时,求取出的卡片上代数式的值为负数的概率.
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.
请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.

答案:
解析
(1) 当$a = 1,b = - 2$时,$a + b = - 1,2a + b = 0,a - b = 3$,即卡片上代数式的值分别是 - 1,0,3. 将三张卡片背面向上并洗匀,从中随机抽取一张,共有 3 种等可能的结果,其中取出的卡片上代数式的值为负数的结果有 1 种,
∴ 取出的卡片上代数式的值为负数的概率为$\frac{1}{3}$.
(2) 补全表格如下:
| 第一次和第二次 | $a + b$ | $2a + b$ | $a - b$ |
|----|----|----|----|
| $a + b$ | $2a + 2b$ | $3a + 2b$ | $2a$ |
| $2a + b$ | $3a + 2b$ | $4a + 2b$ | $3a$ |
| $a - b$ | $2a$ | $3a$ | $2a - 2b$ |
共有 9 种等可能的结果,代数式之和为单项式的结果有 4 种,
∴ 代数式之和为单项式的概率为$\frac{4}{9}$.
(1) 当$a = 1,b = - 2$时,$a + b = - 1,2a + b = 0,a - b = 3$,即卡片上代数式的值分别是 - 1,0,3. 将三张卡片背面向上并洗匀,从中随机抽取一张,共有 3 种等可能的结果,其中取出的卡片上代数式的值为负数的结果有 1 种,
∴ 取出的卡片上代数式的值为负数的概率为$\frac{1}{3}$.
(2) 补全表格如下:
| 第一次和第二次 | $a + b$ | $2a + b$ | $a - b$ |
|----|----|----|----|
| $a + b$ | $2a + 2b$ | $3a + 2b$ | $2a$ |
| $2a + b$ | $3a + 2b$ | $4a + 2b$ | $3a$ |
| $a - b$ | $2a$ | $3a$ | $2a - 2b$ |
共有 9 种等可能的结果,代数式之和为单项式的结果有 4 种,
∴ 代数式之和为单项式的概率为$\frac{4}{9}$.
3.(2023 河北保定模拟)有一个从袋子中摸球的游戏,小红根据游戏规则画出了如图所示的树状图,则此次摸球的游戏规则是( )
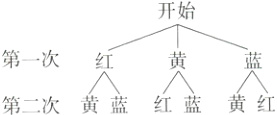
A. 随机摸出一个球后放回,再随机摸出 1 个球
B. 随机摸出一个球后不放回,再随机摸出 1 个球
C. 随机摸出一个球后放回,再随机摸出 2 个球
D. 随机摸出一个球后不放回,再随机摸出 2 个球

A. 随机摸出一个球后放回,再随机摸出 1 个球
B. 随机摸出一个球后不放回,再随机摸出 1 个球
C. 随机摸出一个球后放回,再随机摸出 2 个球
D. 随机摸出一个球后不放回,再随机摸出 2 个球
答案:
B
4.(2024 山西中考)一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同. 从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是( )
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$
答案:
B 列表如下:
| | 红 | 白 | 绿 |
|----|----|----|----|
| 红 | | (红,白) | (红,绿) |
| 白 | (白,红) | | (白,绿) |
| 绿 | (绿,红) | (绿,白) | |
共有 6 种等可能的结果,其中两次摸到的球恰好有一个红球的结果有 (红,白),(红,绿),(白,红),(绿,红),共 4 种,
∴ 两次摸到的球恰好有一个红球的概率为$\frac{4}{6}=\frac{2}{3}$.
| | 红 | 白 | 绿 |
|----|----|----|----|
| 红 | | (红,白) | (红,绿) |
| 白 | (白,红) | | (白,绿) |
| 绿 | (绿,红) | (绿,白) | |
共有 6 种等可能的结果,其中两次摸到的球恰好有一个红球的结果有 (红,白),(红,绿),(白,红),(绿,红),共 4 种,
∴ 两次摸到的球恰好有一个红球的概率为$\frac{4}{6}=\frac{2}{3}$.
5.(2022 湖北仙桃中考)从 2 名男生和 2 名女生中任选 2 名学生参加志愿者服务,那么选出的 2 名学生中至少有 1 名女生的概率是__________.
答案:
答案 $\frac{5}{6}$
解析 画树状图如图所示:

共有 12 种等可能的结果,其中选出的 2 名学生中至少有 1 名女生的结果有 10 种,
∴ 选出的 2 名学生中至少有 1 名女生的概率是$\frac{10}{12}=\frac{5}{6}$.
答案 $\frac{5}{6}$
解析 画树状图如图所示:

共有 12 种等可能的结果,其中选出的 2 名学生中至少有 1 名女生的结果有 10 种,
∴ 选出的 2 名学生中至少有 1 名女生的概率是$\frac{10}{12}=\frac{5}{6}$.
6. 情境题·中华优秀传统文化(2024 四川达州中考)“四大名著”《红楼梦》《水浒传》《三国演义》《西游记》是中华优秀文化的重要组成部分. 某校七年级准备从这四部名著中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本)开展“名著共读”活动,则该年级的学生恰好抽取到《三国演义》和《西游记》的概率是__________.
答案:
答案 $\frac{1}{6}$
解析 记《红楼梦》《水浒传》《三国演义》《西游记》分别为 A、B、C、D,画树状图如下:

由图可得,共有 12 种等可能的结果,其中该年级的学生恰好抽取到《三国演义》和《西游记》的结果有 2 种,故该年级的学生恰好抽取到《三国演义》和《西游记》的概率为$\frac{2}{12}=\frac{1}{6}$.
答案 $\frac{1}{6}$
解析 记《红楼梦》《水浒传》《三国演义》《西游记》分别为 A、B、C、D,画树状图如下:

由图可得,共有 12 种等可能的结果,其中该年级的学生恰好抽取到《三国演义》和《西游记》的结果有 2 种,故该年级的学生恰好抽取到《三国演义》和《西游记》的概率为$\frac{2}{12}=\frac{1}{6}$.
查看更多完整答案,请扫码查看


