《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

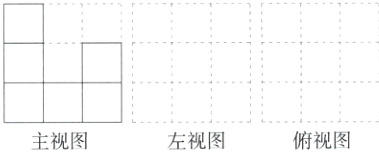
17.(2023浙江金华模拟)(6分)用10个完全相同的小立方体搭成的几何体如图所示.(M9224002)

(1)已知该几何体的主视图如图所示，请在空白的方格中画出它的左视图和俯视图;
(2)若保持主视图和俯视图不变,最多还可以再搭________个小立方体.

答案：
17解析　
(1)如图所示.
　　　　　 　　
(2)3.

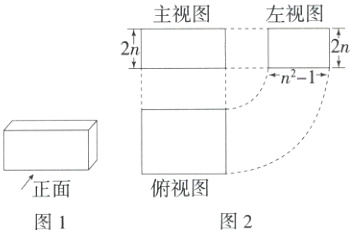
18.(2024河北唐山迁安二模)(8分)图2是图1中长方体的三视图,用S表示面积,且S主 = 2n² + 2n(n＞1).
(1)求S左和S俯;
(2)推断以该长方体的长、宽、高为边能否围成直角三角形.

答案： 18解析　
(1)根据题意，长方体的长为$S_{主}\div(2n)=(2n^3 + 2n)\div(2n)=n^2 + 1$，
$S_{左}=(n^2 - 1)\cdot2n = 2n^3 - 2n$，
$S_{俯}=(n^2 + 1)(n^2 - 1)=n^4 - 1$.
(2)
∵ $(n^2 + 1)^2=n^4 + 2n^2 + 1$，$(n^2 - 1)^2=n^4 - 2n^2 + 1$，$(2n)^2 = 4n^2$，
∴ $(n^2 - 1)^2+(2n)^2=n^4 + 2n^2 + 1=(n^2 + 1)^2$，
∴ 以该长方体的长、宽、高为边能围成直角三角形.

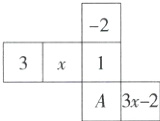
19.(2023山东东营期末)(8分)一个外侧有标记的正方体的平面展开图如图所示，标注了字母A的是正方体的正面,正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和右面标注的数之和.

答案： 19解析根据正方体的表面展开图的特征可知，“A”与“-2”是相对面，“3”与“1”是相对面，“x”与“3x - 2”是相对面.
(1)
∵标注字母A的是正方体的正面，正方体的左面与右面标注的式子相等，
∴x=3x - 2,解得x=1.
(2)
∵标注字母A的是正方体的正面，左面与右面标注的式子相等，
∴上面和右面标注的两个数分别为1和3x - 2或3和x，
∵x=1,
∴1 + 3x - 2 = 2或3 + x = 4.

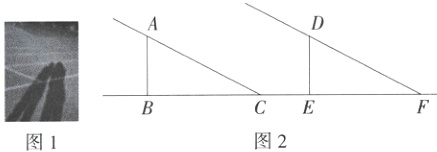
20.(8分)如图1,课间,小明与小亮在操场上突然争论起来，他们都说自己比对方长得高,这时数学老师走过来,笑着对他们说:“你们不要争了,其实你们一样高,瞧瞧地上,你俩的影子一样长!”假定太阳光线是平行的,小聪根据数学老师的解释，画出如图2所示的图形，线段AB表示小明，线段BC表示小明的影子，线段DE表示小亮，线段EF表示小亮的影子，BC = EF,太阳光线AC//DF.请利用全等三角形的有关知识说明小明与小亮一样高.

答案： 20证明　由题知AB⊥BC,DE⊥EF,
∴∠ABC=∠DEF=90°.
∵AC//DF,
∴∠ACB=∠DFE.
在△ABC和△DEF中，$\begin{cases}\angle ABC=\angle DEF,\\BC = EF,\\\angle ACB=\angle DFE\end{cases}$
∴△ABC≌△DEF(ASA),
∴AB=DE,
∴小明与小亮一样高.