第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
23. [答案含评分细则] 新考向·新定义试题(9分)在平面内,先将一个多边形以自身的一个顶点为位似中心放大或缩小,再将所得多边形沿过该点的直线翻折,我们称这种变换为自位似轴对称变换,变换前后的图形成自位似轴对称.例如:如图1,先将△ABC以点A为位似中心缩小,得到△ADE,再将△ADE沿过点A的直线l翻折,得到△AFG,则△ABC和△AFG成自位似轴对称.
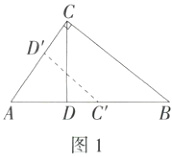
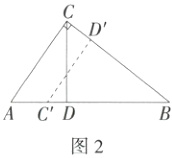
(1)如图2,在△ABC中,∠ACB = 90°,AC<BC,CD⊥AB,垂足为D.下列3对三角形:①△ABC和△ACD;②△BAC和△BCD;③△DAC和△DCB.其中成自位似轴对称的是 .(填序号)
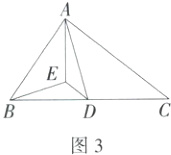
(2)如图3,在△ABC中,D是BC的中点,E为△ABC内一点,∠ABE = ∠C,∠BAE = ∠CAD,连接DE,求证:DE//AC.

(1)如图2,在△ABC中,∠ACB = 90°,AC<BC,CD⊥AB,垂足为D.下列3对三角形:①△ABC和△ACD;②△BAC和△BCD;③△DAC和△DCB.其中成自位似轴对称的是 .(填序号)
(2)如图3,在△ABC中,D是BC的中点,E为△ABC内一点,∠ABE = ∠C,∠BAE = ∠CAD,连接DE,求证:DE//AC.


答案:
解析
(1)由图1,2,可知△ABC和△ACD,△BAC和△BCD成自位似轴对称.
故答案为①②. ………………………………… 2分
(2)证明:如图,延长BE交AC于F,
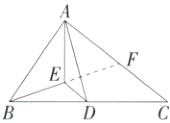
……………………………………………… 3分
∵∠ABE = ∠C,∠BAE = ∠CAD,
∴△ABE∽△ACD,
∴BE/CD = AE/AD,…………………………………… 5分
∵∠BAE = ∠CAD,
∴∠BAE + ∠DAE = ∠CAD + ∠DAE,
∴∠BAD = ∠FAE,
∵∠AEF = ∠ABE + ∠BAE,∠ADB = ∠CAD + ∠C,
∴∠AEF = ∠ADB,
∴△EAF∽△DAB,
∴EF/BD = AE/AD,
∴BE/CD = EF/BD. ……………………… 8分
∵点D是BC的中点,
∴CD = BD,
∴BE = EF,
∴DE//AC. ……………………… 9分
解析
(1)由图1,2,可知△ABC和△ACD,△BAC和△BCD成自位似轴对称.


故答案为①②. ………………………………… 2分
(2)证明:如图,延长BE交AC于F,

……………………………………………… 3分
∵∠ABE = ∠C,∠BAE = ∠CAD,
∴△ABE∽△ACD,
∴BE/CD = AE/AD,…………………………………… 5分
∵∠BAE = ∠CAD,
∴∠BAE + ∠DAE = ∠CAD + ∠DAE,
∴∠BAD = ∠FAE,
∵∠AEF = ∠ABE + ∠BAE,∠ADB = ∠CAD + ∠C,
∴∠AEF = ∠ADB,
∴△EAF∽△DAB,
∴EF/BD = AE/AD,
∴BE/CD = EF/BD. ……………………… 8分
∵点D是BC的中点,
∴CD = BD,
∴BE = EF,
∴DE//AC. ……………………… 9分
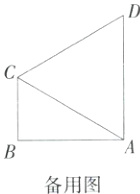
24. [答案含评分细则] 数学文化·费马点(2024山东潍坊潍城二模)(10分)在△ABC中,∠B = 90°,AB = 4√3,BC = 4,以AC为边在△ABC外作等边三角形ACD,点G是△ABC内部或边上一点,连接AG,CG,线段AG绕点A顺时针旋转60°后的对应线段为AM,连接DM.
(1)在图1中,若点G在边AB上,则线段DM与线段CG之间的数量关系是 ,线段DM与线段CG所在的两条直线相交所形成的锐角的度数为 ;
(2)在图2中,若点G在△ABC内部,判断(1)中的结论是否成立,并说明理由;
(3)在(2)的条件下,连接GB,求GA + GB + GC的最小值,并说明此时CG//AM.

(1)在图1中,若点G在边AB上,则线段DM与线段CG之间的数量关系是 ,线段DM与线段CG所在的两条直线相交所形成的锐角的度数为 ;
(2)在图2中,若点G在△ABC内部,判断(1)中的结论是否成立,并说明理由;
(3)在(2)的条件下,连接GB,求GA + GB + GC的最小值,并说明此时CG//AM.


答案:
解析
(1)DM = CG;60°. ……………………… 2分
(2)成立,理由:延长DM交CG的延长线于Q, …
……………………………………………… 3分
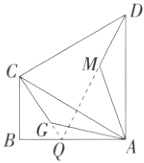
∵线段AG绕点A顺时针旋转60°后的对应线段为AM,
∴AG = AM,∠GAM = 60°,
∵△ACD是等边三角形,
∴AC = AD,∠CAD = 60°,
∴∠GAM = ∠CAD,
∴∠GAC = ∠MAD,
∴△GAC≌△MAD,
∴DM = CG,∠ADM = ∠ACG,
∴∠CQM = ∠CAD = 60°.故
(1)中的结论成立. ……
……………………………………………… 6分
(3)如图,连GM,BD,
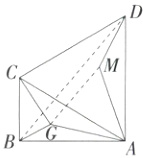
由
(2)知CG = DM,△AGM是等边三角形,
∴GA = GM,
∴GA + GB + GC = BG + GM + MD,
∴当点G、M在线段BD上时,BG + GM + MD = BD,此时GA + GB + GC的值最小,…………………… 7分
∵∠ABC = 90°,AB = 4√3,BC = 4,
∴AC = 8,∠BAC = 30°,
∴∠BAD = 90°,
∴BD = √(8² + (4√3)²) = 4√7,
∴GA + GB + GC的最小值为4√7.
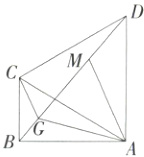
如图,由△AMD≌△AGC可知,∠AMD = ∠AGC = 120°,
∴∠AGC + ∠GAM = 180°,
∴CG//AM.
……………………………………………… 10分
解析
(1)DM = CG;60°. ……………………… 2分
(2)成立,理由:延长DM交CG的延长线于Q, …
……………………………………………… 3分

∵线段AG绕点A顺时针旋转60°后的对应线段为AM,
∴AG = AM,∠GAM = 60°,
∵△ACD是等边三角形,
∴AC = AD,∠CAD = 60°,
∴∠GAM = ∠CAD,
∴∠GAC = ∠MAD,
∴△GAC≌△MAD,
∴DM = CG,∠ADM = ∠ACG,
∴∠CQM = ∠CAD = 60°.故
(1)中的结论成立. ……
……………………………………………… 6分
(3)如图,连GM,BD,

由
(2)知CG = DM,△AGM是等边三角形,
∴GA = GM,
∴GA + GB + GC = BG + GM + MD,
∴当点G、M在线段BD上时,BG + GM + MD = BD,此时GA + GB + GC的值最小,…………………… 7分
∵∠ABC = 90°,AB = 4√3,BC = 4,
∴AC = 8,∠BAC = 30°,
∴∠BAD = 90°,
∴BD = √(8² + (4√3)²) = 4√7,
∴GA + GB + GC的最小值为4√7.
如图,由△AMD≌△AGC可知,∠AMD = ∠AGC = 120°,
∴∠AGC + ∠GAM = 180°,
∴CG//AM.

……………………………………………… 10分
查看更多完整答案,请扫码查看


