《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

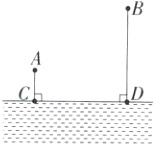
8.(最短距离问题 教材变式·P23T2)如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC = 1千米,BD = 3千米,CD = 3千米.现要在河边CD上建造一水厂,向A、B两村送自来水(水管需直接到A、B村).
(1)水厂应修建在什么地方,可使所用的水管最短(请你在图中设计出水厂的位置)?
(2)如果铺设水管的工程费用为每千米20 000元,为使铺设水管的费用最节省,请求出最节省的铺设水管的费用.

答案：
解析 （1）如图，作点A关于CD的对称点M，连接BM交CD于点P，点P就是水厂的位置.
　　　　　　　
（2）如图，过点M作MN⊥BD交BD的延长线于N.
在Rt△BMN中，BN=3 + 1 = 4千米，MN=3千米，
∴ MB=$\sqrt{MN^{2}+BN^{2}}$=5（千米），
∴ AP+BP=MB=5千米，
∴ 最节省的铺设水管的费用为20000×5=100000（元）.

9.(2023北京北师大实验中学期中)已知A、B两点的坐标分别是(-1,3)和(1,3),则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B之间的距离为2;④A、B之间的距离为6.其中正确的是(　　　)
A.①④
B.①③
C.②④
D.②③

答案： D
∵ A、B两点的坐标分别是(-1，3)和(1，3)，纵坐标相等，横坐标互为相反数，
∴ A、B两点关于y轴对称，故①错误，②正确；A、B之间的距离为1 - (-1)=2，故③正确，④错误.故选D.

10.(2024广西贺州三模)已知点P(2,-3)与点Q(2,3)关于某条直线对称,则这条直线是(M9223005)(　　　)
A.x轴
B.y轴
C.过点(2,0)且垂直于x轴的直线
D.过点(0,-3)且平行于x轴的直线

答案： A
∵点P(2，-3)，点Q(2，3)，
∴ PQ//y轴.设PQ的中点为M，则M点的坐标为$(2,\frac{-3 + 3}{2})$，即(2，0)，
∴点P(2，-3)与点Q(2，3)关于经过点(2，0)且垂直于y轴的直线对称，即点P(2，-3)与点Q(2，3)关于x轴对称，故A正确.

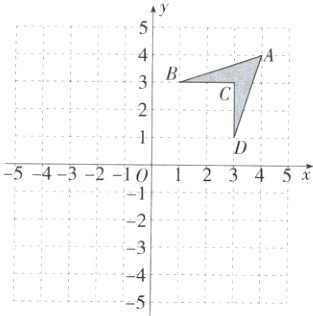
11.(2023北京石油附中期中)如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).(M9223005)
(1)画出四边形A1B1C1D1,使它与“基本图形”关于x轴对称,并求出A1,B1的坐标A1(____,____),B1(____,____);
(2)画出四边形A2B2C2D2,使它与“基本图形”关于y轴对称,并求出C2,D2的坐标C2(____,____),D2(____,____);
(3)画出四边形A3B3C3D3,使它与前面三个图形组成的图形是轴对称图形.

答案：
解析 （1）如图，四边形A₁B₁C₁D₁即为所求作的图形，A₁(4，-4)，B₁(1，-3).
（2）如图，四边形A₂B₂C₂D₂即为所求作的图形，C₂(-3，3)，D₂(-3，1).
（3）答案不唯一.如图所示，四边形A₃B₃C₃D₃即为所求作的图形.

12.(2023北京中考,2,★☆☆)下列图形中,既是轴对称图形又是中心对称图形的是(　　　)

答案： 12A A.既是轴对称图形又是中心对称图形；B.是中心对称图形，不是轴对称图形；C.是轴对称图形，不是中心对称图形；D.是轴对称图形，不是中心对称图形.

13.(新考向·规律探究题)(2024北京陈经纶中学期中,8,★☆☆)已知点E(x0,y0),F(x2,y2),点M(x1,y1)是线段EF的中点,则x1 = $\frac{x_{0}+x_{2}}{2}$,y1 = $\frac{y_{0}+y_{2}}{2}$.在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA = P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2024的坐标是(　　　)
A.(0,0)
B.(0,2)
C.(2,-4)
D.(-4,2)

答案： 13D 设P₁(x，y)，
∵点P(0，2)关于点A的对称点为P₁，
∴点A为点P和点P₁的中点，
∵A(1，-1)，
∴ $\frac{x + 0}{2}=1$，$\frac{y + 2}{2}=-1$，
∴ x=2，y=-4，
∴ P₁(2，-4)，同理可得P₂(-4，2)，P₃(4，0)，P₄(-2，-2)，P₅(0，0)，P₆(0，2)，P₇(2，-4)，……，
∴ 每6次为一个循环，
∵ $\frac{2024}{6}=337\cdots\cdots2$，
∴ P₂₀₂₄(-4，2)，
∴ 点P₂₀₂₄的坐标是(-4，2).
故选D.