《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

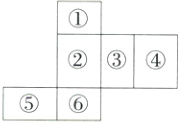
9.如图所示的是一个多面体的表面展开图，每个面都标注了数字.若多面体的底面是面③，则多面体的上面是面_______.(填数字序号)
　　　　　　

答案： 答案　⑤

10.(2024北京门头沟二模)某函数图象满足过点(0,2)，且当x ＞ 0时，y随x的增大而增大，写出一个满足条件的表达式：_______.

答案： 答案y = x² + 2(答案不唯一)

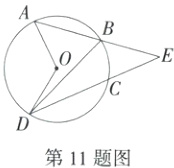
11.(2024北京广渠门中学二模)如图，⊙O的弦AB、DC的延长线相交于点E，∠AOD = 128°，∠E = 40°，则∠BDC = _______°.
　　

答案： 答案　24
　解析
∵ ∠ABD = 1/2∠AOD，∠AOD = 128°，
∴ ∠ABD = 64°，
∵ ∠E = 40°，
∴ ∠BDC = ∠ABD - ∠E = 64° - 40° = 24°.

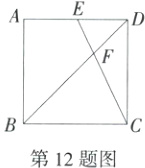
12.(2024北京平谷二模)如图，正方形ABCD的边长为3，点E为AD边的中点，连接BD、CE，BD与CE相交于点F，则DF的长为_______.
　　

答案： 答案　√2
　解析
∵ 四边形ABCD为正方形，
∴ AD = BC = 3，AD //BC，∠CBD = 45°，∠BCD = 90°，
∴ BD = BC/cos45° = 3√2.
∵ 点E为AD边的中点，
∴ DE = 3/2.
∵ AD//BC，
∴ ∠EDF = ∠CBF，∠DEF = ∠BCF，
∴ △DEF∽△BCF，
∴ DF/BF = DE/BC，即DF/(3√2 - DF) = 3/2，解得DF = √2.

13.(2024北京门头沟一模)已知一元二次方程x² + ax + b = 0有两个根，两根之和为正数，两根之积是负数，写出一组符合条件的a、b的值：_______.

答案： 答案　a = -1，b = -2(答案不唯一)
　　解析
∵ 一元二次方程x² + ax + b = 0有两个根，
　
∴ a² - 4b≥0，
∴ 4b≤a²，
　
∵ 两根之和为正数，两根之积是负数，
　
∴ -a＞0，b＜0，
∴ a＜0，
∴ a = -1，b = -2.(答案不唯一)

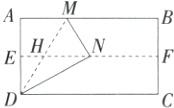
14.(2024北京北师大实验中学期中)将矩形ABCD对折，使AB与DC重合，得到折痕EF，把纸片展平，再次折叠，使点A落在折痕EF上，并使折痕经过点D，得到折痕DM和线段DN，记DM与EF的交点为H.若AD = 2√3，则HN = _______.
　　　　　　

答案： 答案　2
　　解析　由折叠的性质可得AE = DE = 1/2AD = √3，AD = DN = 2√3，∠EDH = 1/2∠ADN，∠DEF = 90°，
∴ DE = 1/2DN，
∴ sin∠DNE = DE/DN = 1/2，
∴ ∠DNE = 30°，
　
∵ ∠DEN = 90°，
∴ ∠ADN = 60°，
∴ EN = DN·sin∠EDN = 2√3·sin60° = 2√3×√3/2 = 3，∠EDH = 30°，
　
∴ EH = DE·tan∠EDH = √3·tan30° = √3×√3/3 = 1，
　
∴ HN = EN - EH = 3 - 1 = 2.

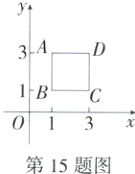
15.[新考向·规律探究题][新独家原创]规定：在平面直角坐标系xOy中，把某一图形先关于原点对称，再沿y轴翻折为一次变换.如图，已知正方形ABCD，顶点A(1,3)，C(3,1)，若正方形ABCD经过一次上述变换，则点A变换后的坐标为_______；对正方形ABCD连续经过2 024次这样的变换，点D变换后的坐标为_______.
　　　

答案： 答案　(1,-3)；(3,3)
　　解析　根据平面直角坐标系内关于原点和y轴对称的点的坐标特征可知，点A(1,3)先关于原点对称，再沿y轴翻折后的坐标为(1,-3).由题意得D(3,3).将正方形ABCD经过一次变换后D点坐标变为(3,-3)，经过两次变换后D点坐标变为(3,3)，经过三次变换后D点坐标变为(3,-3)，……，故连续经过2024次这样的变换，点D变换后的坐标为(3,3).

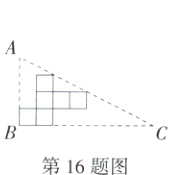
16.(2024吉林长春一零八中模拟)如图，在直角三角形ABC纸片上剪出如图所示的正方体的展开图，直角三角形的两直角边与正方体展开图左下角正方形的边重合，斜边恰好经过两个正方形的顶点.已知BC = 12 cm，则这个展开图中正方形的边长是_______cm.
　　　

答案：
答案　1.5
　　解析　如图，设这个展开图中正方形的边长为xcm，延长FH交AB于点D，则EF = BD = 2xcm，EG = xcm，DF = 4xcm，
∵ DF//BC，
∴ ∠EFG = ∠C，
∵ tan∠EFG = EG/EF = 1/2，
∴ tan∠C = AB/BC = 1/2，
∵ BC = 12cm，
∴ AB = 6cm，
∴ AD = AB - BD = (6 - 2x)cm，
∵ DF//BC，
∴ △ADF∽△ABC，
∴ DF/BC = AD/AB，即4x/12 = (6 - 2x)/6，解得x = 1.5，即这个展开图中正方形的边长为1.5cm.
　　　　　　　

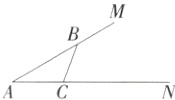
17.[答案含评分细则][新考向·尺规作图](5分)如图，∠MAN = 30°，点B、C分别在AM、AN上，且∠ABC = 40°.
(1)尺规作图：作∠CBM的平分线BD，BD与AN相交于点D；(保留作图痕迹，不写作法)
(2)在(1)所作的图中，求证：△ABC∽△ADB.
　　　　　　　　　　　

答案：
解析　
(1)如图所示，线段BD即为所求.

　　　　　　　　　　　　　　　　　　　2分
(2)证明:
∵ ∠ABC = 40°，
∴ ∠MBC = 140°，
　
∵ BD平分∠MBC，
∴ ∠MBD = 1/2∠MBC = 70°，
　
∵ ∠MBD是△ADB的一个外角，
　
∴ ∠ADB = ∠MBD - ∠A = 70° - 30° = 40°，
　
∴ ∠ABC = ∠ADB.
　
∵ ∠A = ∠A，
∴ △ABC∽△ADB.　　　　　　　5分