第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
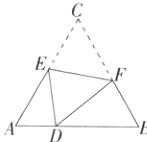
8.(2023北京顺义期中)如图,将等边△ABC折叠,使点C落在AB边上的点D处,折痕为EF,点E,F分别在AC和BC边上. 若AC = 8,AD = 2,则△AED的周长为________,$\frac{CE}{CF}$的值为________.(M9223004)

答案:
答案 10;$\frac{5}{7}$
解析
∵ △ABC是等边三角形,
∴ BC = AB = AC = 8,∠ABC = ∠ACB = ∠BAC = 60°,
∵ AD = 2,
∴ BD = 6,由折叠的性质得,CE = DE,CF = DF,∠EDF = ∠C = 60°,
∴ AE + DE + AD = AC + AD = 10,即△AED的周长为10,
∴ DF + BF + BD = BC + BD = 14,即△DFB的周长为14.
∵ ∠EDF = ∠BAC = ∠ABC = 60°,
∴ ∠FDB + ∠EDA = ∠AED + ∠EDA = 120°,
∴ ∠FDB = ∠AED.
∵ ∠B = ∠A = 60°,
∴ △AED∽△BDF,
∴ (AE + DE + AD) : (DF + BF + BD) = DE : DF = CE : CF,
∴ $\frac{CE}{CF}=\frac{10}{14}=\frac{5}{7}$.
解析
∵ △ABC是等边三角形,
∴ BC = AB = AC = 8,∠ABC = ∠ACB = ∠BAC = 60°,
∵ AD = 2,
∴ BD = 6,由折叠的性质得,CE = DE,CF = DF,∠EDF = ∠C = 60°,
∴ AE + DE + AD = AC + AD = 10,即△AED的周长为10,
∴ DF + BF + BD = BC + BD = 14,即△DFB的周长为14.
∵ ∠EDF = ∠BAC = ∠ABC = 60°,
∴ ∠FDB + ∠EDA = ∠AED + ∠EDA = 120°,
∴ ∠FDB = ∠AED.
∵ ∠B = ∠A = 60°,
∴ △AED∽△BDF,
∴ (AE + DE + AD) : (DF + BF + BD) = DE : DF = CE : CF,
∴ $\frac{CE}{CF}=\frac{10}{14}=\frac{5}{7}$.
9.(2023北京朝阳期中)如图,对正方形纸片ABCD进行如下折叠:
①先对折,使AB与CD重合,得到折痕EF;
②折叠纸片,使点A落在EF上的点H处,点D也落在EF上的点H处,沿BH和CH剪下△BCH.
判定△BCH为等边三角形的依据是(M9223004) ( )
A. 三个角都相等的三角形是等边三角形
B. 有两个角是60°的三角形是等边三角形
C. 三边都相等的三角形是等边三角形
D. 有一个角是60°的等腰三角形是等边三角形

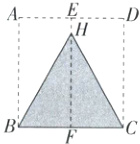
①先对折,使AB与CD重合,得到折痕EF;
②折叠纸片,使点A落在EF上的点H处,点D也落在EF上的点H处,沿BH和CH剪下△BCH.
判定△BCH为等边三角形的依据是(M9223004) ( )
A. 三个角都相等的三角形是等边三角形
B. 有两个角是60°的三角形是等边三角形
C. 三边都相等的三角形是等边三角形
D. 有一个角是60°的等腰三角形是等边三角形


答案:
C
∵ 四边形ABCD是正方形,
∴ AB = BC = CD = DA,由翻折变换可得,AB = HB,
∴ BH = BC,
∵ EF是BC的垂直平分线,
∴ BH = CH,
∴ BH = CH = BC,
∴ △BHC是等边三角形,故选C.
∵ 四边形ABCD是正方形,
∴ AB = BC = CD = DA,由翻折变换可得,AB = HB,
∴ BH = BC,
∵ EF是BC的垂直平分线,
∴ BH = CH,
∴ BH = CH = BC,
∴ △BHC是等边三角形,故选C.
10.(2022北京首师大附中期中)如图,将Rt△ABC折叠,使直角顶点C落在斜边AB上的点E处,折痕为BD,连接CE,现有以下结论:
①DE⊥AB;
②BC = BE;
③BD平分∠ABC;
④△BCE是等边三角形;
⑤BD垂直平分EC.
其中正确的结论是(M9223004) ( )
A. ①②③ B. ②③ C. ①②③④ D. ①②③⑤
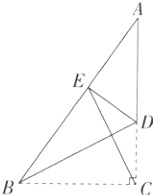
①DE⊥AB;
②BC = BE;
③BD平分∠ABC;
④△BCE是等边三角形;
⑤BD垂直平分EC.
其中正确的结论是(M9223004) ( )
A. ①②③ B. ②③ C. ①②③④ D. ①②③⑤

答案:
D
∵ 将Rt△ABC折叠,使直角顶点C落在斜边AB上的点E处,
∴ △BCD≌△BED,
∴ ∠BED = ∠BCD = 90°,BC = BE,∠CBD = ∠EBD,DE = DC,
∴ DE⊥AB,BD平分∠ABC,故①②③正确;
∵ DE = DC,BE = BC,
∴ BD垂直平分EC,故⑤正确;
∵ ∠ABC不一定等于60°,
∴ △BCE不一定是等边三角形,故④错误. 故选D.
∵ 将Rt△ABC折叠,使直角顶点C落在斜边AB上的点E处,
∴ △BCD≌△BED,
∴ ∠BED = ∠BCD = 90°,BC = BE,∠CBD = ∠EBD,DE = DC,
∴ DE⊥AB,BD平分∠ABC,故①②③正确;
∵ DE = DC,BE = BC,
∴ BD垂直平分EC,故⑤正确;
∵ ∠ABC不一定等于60°,
∴ △BCE不一定是等边三角形,故④错误. 故选D.
11. 甲乙丙三人用同一张矩形纸张接力进行如图所示的操作:甲任意画一个△ABC,折叠纸张,使得点A与点C重合,折痕与AC边交于点O;乙再折出射线BO,点E在BO的延长线上;丙再折叠纸张,使得OB落在OE上,点B的对应点为点D,连接AD,DC. 下列说法错误的是( )
A. 四边形ABCD为平行四边形
B. 在△ABC中,若∠BAC + ∠ACB = 90°,则四边形ABCD为矩形
C. 若AC = 2OB,则四边形ABCD为正方形
D. 若射线BO平分∠ABC,则四边形ABCD为菱形
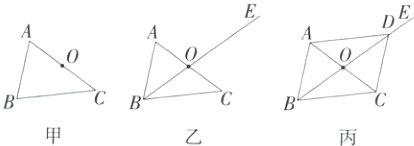
A. 四边形ABCD为平行四边形
B. 在△ABC中,若∠BAC + ∠ACB = 90°,则四边形ABCD为矩形
C. 若AC = 2OB,则四边形ABCD为正方形
D. 若射线BO平分∠ABC,则四边形ABCD为菱形

答案:
C 由OA = OC,OB = OD,可得四边形ABCD为平行四边形,A说法正确;在△ABC中,若∠BAC + ∠ACB = 90°,则∠ABC = 90°,则平行四边形ABCD为矩形,B说法正确;若AC = 2OB,则AC = BD,则平行四边形ABCD为矩形,不能得到四边形ABCD为正方形,C说法错误;若射线BO平分∠ABC,则平行四边形ABCD中,∠ABO = ∠CBO = ∠ADO,则AB = AD,则四边形ABCD为菱形,D说法正确.
故选C.
故选C.
查看更多完整答案,请扫码查看


