《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

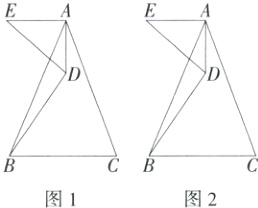
14. [北京常考·图形变换题]（2024北京石景山一模，27，★★☆）在△ABC中，AB = AC，0° ＜ ∠BAC ＜ 60°，将线段BC绕点B逆时针旋转60°得到线段BD，连接AD. 将线段AD绕点A顺时针旋转90°得到线段AE，连接DE.
（1）如图1，求证：EA//BC.
（2）延长BC到点F，使得CF = CB，连接DF交AC于点M，依题意补全图2. 若点M是AC的中点，用等式表示线段MF，MD，DE之间的数量关系，并证明.

答案：
解析
(1)证明：延长AD交BC于点G，连接CD，如图1.

∵BD = BC，∠DBC = 60°，
∴△DBC是等边三角形，
∴DC = DB = BC，∠DCB = 60°，
∴点D在线段BC的垂直平分线上.
∵AB = AC，
∴点A在线段BC的垂直平分线上，
∴AG⊥BC，
∴∠AGC = 90°.
∵∠AGC = ∠GAE = 90°，
∴EA//BC.
(2)依题意补全题图2，如图2.
数量关系：MF = MD + $\sqrt{2}$DE.
证明：延长FD交AE的延长线于点N，连接CD，如图2.

∵DC = BC，CF = BC，
∴CF = CD，
∴∠F = ∠FDC = $\frac{1}{2}$∠1 = 30°.
∵EA//BC，
∴∠N = ∠F = 30°.
又
∵∠AMN = ∠CMF，AM = CM，
∴△AMN≌△CMF，
∴MF = MN.
在Rt△EAD中，AE = AD，
∴DE = $\sqrt{2}$AD，
在Rt△NAD中，∠N = 30°，
∴DN = 2AD，
∴DN = $\sqrt{2}$DE，
∴MN = MD + DN = MD + $\sqrt{2}$DE，
∴MF = MD + $\sqrt{2}$DE.

1. 如图，在5×5的方格纸中，A，B两点在格点上，线段AB绕某点（旋转中心）逆时针旋转角α后得到线段A'B'，点A'与A对应，则旋转中心是 （ ）

A.点B
B.点G
C.点E
D.点F

答案：
C 如图，连接AA'，BB'，作线段AA'，BB'的垂直平分线，交点为E，则点E即为旋转中心.故选C.

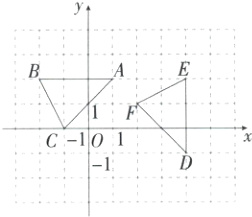
2. 如图，△ABC绕某点旋转，得到△DEF，则旋转中心的坐标是 （ ）

A.（1，0）
B.（1，-1）
C.（0，-1）
D.（0，0）

答案：
B 如图，连接AD，BE，作线段AD、BE的垂直平分线，交点为O'，点O'即为旋转中心.由图可知点O'的坐标为(1,-1).

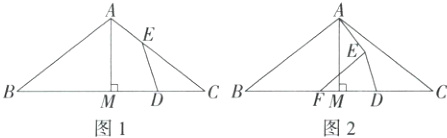
15. [推理能力]（2023北京中考）在△ABC中，∠B = ∠C = α（0° ＜ α ＜ 45°），AM⊥BC于点M，D是线段MC上的动点（不与点M，C重合），将线段DM绕点D顺时针旋转2α得到线段DE.
（1）如图1，当点E在线段AC上时，求证：D是MC的中点；
（2）如图2，若在线段BM上存在点F（不与点B，M重合）满足DF = DC，连接AE，EF，直接写出∠AEF的大小，并证明.

答案：
解析
(1)证明：由旋转的性质得DM = DE，∠MDE = 2α，
∵∠C = α，
∴∠DEC = ∠MDE - ∠C = α，
∴∠C = ∠DEC，
∴DE = DC，
∴DM = DC，即D是MC的中点.
(2)∠AEF = 90°.
证明：如图，延长FE到H，使EH = FE，连接CH，AH，AF.

∵DF = DC，FE = EH，
∴DE是△FCH的中位线
∴DE//CH，CH = 2DE，
由旋转的性质得，DM = DE，∠MDE = 2α，
∴∠FCH = 2α，
∵∠B = ∠ACB = α，
∴AB = AC，∠ACH = ∠BCH - ∠ACB = α，
∴∠B = ∠ACH，
设DM = DE = m，CD = n，
则CH = 2m，CM = m + n，DF = CD = n，
∴FM = DF - DM = n - m，
∵AB = AC，AM⊥BC，
∴BM = CM = m + n，
∴BF = BM - FM = m + n - (n - m) = 2m，
∴CH = BF.
在△ABF和△ACH中，
∵$\begin{cases}AB = AC,\\\angle B = \angle ACH,\\BF = CH,\end{cases}$
∴△ABF≌△ACH(SAS)，
∴AF = AH，
∵FE = EH，
∴AE⊥FH，即∠AEF = 90°.