《2025年5年中考3年模拟九年级数学下册北京课改版北京专版》

1. 跨化学·溶液（2024河北二模）化学实验室的试管架上放有4支完全相同的试管，试管中分别装有等量的4种无色无味的溶液，其中1支装有酸溶液，2支装有盐溶液，1支装有碱溶液. 若从中随机选取1支试管，则该支试管中装有盐溶液的概率为（ ）
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. 1

答案： A 由题意可得，从中随机选取1支试管，该支试管中装有盐溶液的概率为$\frac{2}{1 + 2 + 1}=\frac{2}{4}=\frac{1}{2}$，故选A。

2. 教材变式·P62探索（2023北京中考）先后两次抛掷同一枚质地均匀的硬币，则第一次正面向上、第二次反面向上的概率是（M9225001）（ ）
A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{3}{4}$

答案： A 先后两次抛掷同一枚质地均匀的硬币，总共有四种等可能的结果，分别是(正,正)，(正,反)，(反，正)，(反，反)，则第一次正面向上、第二次反面向上的概率是$\frac{1}{4}$，故选A。

3. 教材变式·P65T2 如图所示的五张卡片（除正面图案外完全相同）分别印有巴黎奥运会的项目图标：篮球、跳水、赛跑、骑行和花样游泳，其中跳水和花样游泳是水上项目，现将五张卡片背面朝上放置，打乱后随机抽取一张，抽到的卡片上的图标恰好是水上项目的概率是______.

答案： 答案$\frac{2}{5}$
解析
∵ 共5张卡片，其中印有水上项目的有2张，
∴ 打乱后随机抽取一张，抽到的卡片上的图标恰好是水上项目的概率是$\frac{2}{5}$。

4.（2024北京中考，5，★☆☆）不透明袋子中仅有红、黄小球各一个，两个小球除颜色外无其他差别. 从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，则两次摸出的都是红球的概率是（ ）
A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{3}{4}$

答案： A 由题意得，共有4种等可能的结果：(红，红)，(红,黄)，(黄,红)，(黄,黄)，其中两次摸出的都是红球的结果有1种，
∴ 两次摸出的都是红球的概率为$\frac{1}{4}$。故选A。

5.（2024北京门头沟二模，7，★☆☆）小明去商场购物，购买完后商家有一个抽奖答谢活动，有m张奖券，其中含奖项的奖券有n张，每名已购物的顾客只能抽取一次，小明抽之前有10名顾客已经抽过奖，中奖的有3人，则小明中奖的概率为（ ）
A. $\frac{n}{m}$
B. $\frac{n}{m - 10}$
C. $\frac{n - 3}{m - 10}$
D. $\frac{n - 3}{m}$

答案： C 由题意得，小明中奖的概率=$\frac{n - 3}{m - 10}$。故选C。

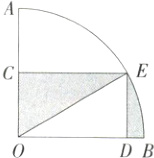
6.（2024山东威海中考，6，★☆☆）如图，在扇形AOB中，∠AOB = 90°，点C是AO的中点. 过点C作CE⊥AO交$\overset{\frown}{AB}$于点E，过点E作ED⊥OB，垂足为点D. 在扇形内随机选取一点P，则点P落在阴影部分的概率是（M9225001）（ ）

A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$

答案： B  设$OA = OE = OB = r$，
∵$CE\perp AO$，
∴$\angle OCE = 90^{\circ}$，
∵ 点C是AO的中点，
∴$OC=\frac{1}{2}OA=\frac{1}{2}OE$。
在$Rt\triangle OCE$中，
∵$\cos\angle COE=\frac{OC}{OE}=\frac{1}{2}$，
∴$\angle COE = 60^{\circ}$，
∴$\angle BOE=\angle AOB-\angle COE = 30^{\circ}$，
∵$ED\perp OB$，
∴$\angle ODE = 90^{\circ}$，
∵$\angle COD=\angle OCE = 90^{\circ}$，
∴ 四边形OCED为矩形，
∴$S_{\triangle OCE}=S_{\triangle ODE}$，
∴ 阴影部分的面积=$S_{扇形BOE}=\frac{30\times\pi\times r^{2}}{360}$，
∴ 点P落在阴影部分的概率=$\frac{S_{扇形BOE}}{S_{扇形AOB}}=\frac{\frac{30\times\pi\times r^{2}}{360}}{\frac{90\times\pi\times r^{2}}{360}}=\frac{1}{3}$。故选B。