《2025年课堂点睛八年级数学下册人教版安徽专版》

1. 随着暑假临近，某游泳馆推出了甲、乙两种消费卡，设消费次数为x时，所需费用为y元，且y与x的函数关系如图所示. 根据图中信息判断，下列说法错误的是 （ ）

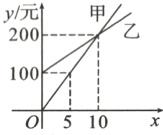
A. 消费次数为10时，选择甲、乙两种消费卡所需费用一样
B. 消费次数为6时，选择甲种消费卡合算
C. 消费次数为15时，选择乙种消费卡合算
D. 消费次数为2时，选择乙种消费卡所需费用为150元

答案： 1.D

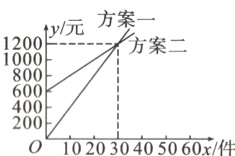
2.（丽水市中考）我市“共富工坊”问海借力，某公司产品销售量得到大幅提升. 为促进生产，该公司提供了两种付给员工月报酬的方案，如图所示，员工可以任选一种方案与公司签订合同. 解答下列问题：
（1）求方案二中y关于x的函数解析式；
（2）如果你是劳务服务部门的工作人员，你如何指导员工根据自己的生产能力选择方案？

答案：
(1)解:设方案二中y关于x的函数解析式为y = kx + b(k≠0).将(0,600),(30,1200)分别代入,得$\begin{cases}b = 600\\30k + b = 1200\end{cases}$,解得$\begin{cases}k = 20\\b = 600\end{cases}$.所以方案二中y关于x的函数解析式为y = 20x + 600.
(2)由两种方案的图象交点(30,1200)可知:若生产件数x的取值范围为$0\leq x＜30$,则选择方案二;若生产件数x = 30,则选择两个方案都可以;若生产件数x的取值范围为$x＞30$,则选择方案一.

3.（凉山州中考）为全面贯彻党的教育方针，严格落实教育部对中小学生“五项管理”的相关要求和《关于进一步加强中小学生体质健康管理工作的通知》精神，保障学生每天在校1小时体育活动时间，某班计划采购A、B两种类型的羽毛球拍，已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元；购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.
（1）求A、B两种类型羽毛球拍的单价.
（2）该班准备采购A、B两种类型的羽毛球拍共30副，且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍，请给出最省钱的购买方案，求出最少费用，并说明理由.

答案：
(1)解:设A型羽毛球拍的单价为每副x元,B型羽毛球拍的单价为每副y元.由题意,得$\begin{cases}3x + 4y = 248\\5x + 2y = 264\end{cases}$,解得$\begin{cases}x = 40\\y = 32\end{cases}$.答:A型羽毛球拍的单价为每副40元,B型羽毛球拍的单价为每副32元.
(2)设该班采购A型羽毛球拍m副,购买的费用为W元,则采购B型羽毛球拍(30 - m)副,由
(1)的结论得W = 40m + 32(30 - m)=8m + 960.
∵A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,
∴$\begin{cases}m\geq2(30 - m)\\30 - m＞0\end{cases}$,解得$20\leq m＜30$.在$20\leq m＜30$内,W随m的增大而增大.则当m = 20时,W取得最小值,最小值为$8×20 + 960 = 1120$.此时$30 - m = 30 - 20 = 10$.答:最省钱的购买方案是采购20副A型羽毛球拍,10副B型羽毛球拍;最少费用为1120元.