《2025年课堂点睛八年级数学下册人教版安徽专版》

13.计算：
（1）$\sqrt{16}-\sqrt{(-3)^{2}}+3\sqrt{(-\frac{1}{3})^{2}}$；
（2）$(-1)^{2025}+(3 - \pi)^{0}-(\frac{1}{3})^{-1}+(\sqrt{3}-\sqrt{3})^{2}$.

答案：
(1)解:原式 =4 - 3+3×$\frac{1}{3}$=2;
(2)解:原式 = - 1+1 - 3+3 - $\sqrt{3}$= - $\sqrt{3}$.

14.（核心素养·推理能力）若$a$，$b$，$c$为$\triangle ABC$的三边长，$a$和$b$满足$b^{2}+\sqrt{a - 6}+4 = 4b$，求$c$的取值范围.

答案： 解:
∵$b^{2}+\sqrt{a - 6}+4 = 4b$,
∴$b^{2}-4b + 4+\sqrt{a - 6}=0$,即$(b - 2)^{2}+\sqrt{a - 6}=0$,
∴$b - 2=0,a - 6=0$,
∴$b = 2,a = 6$.
∵a,b,c为△ABC 的三边长,
∴$a - b ＜ c ＜ a + b$.
∴$4 ＜ c ＜ 8$.

15.若点$P(m,n)$在第二象限，则化简$\sqrt{m^{2}}+\sqrt{n^{2}}$的结果为（ ）
A.$m + n$
B.$m - n$
C.$-m + n$
D.$-m - n$

答案： C

【变式】如图，数轴上点$A$表示的数为$a$，则化简$\sqrt{(a - 3)^{2}}-\sqrt{(a - 4)^{2}}$的结果为________.

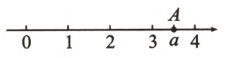
答案： 2a−7

16.已知$a$，$b$，$c$是$\triangle ABC$的三边长，则化简$\sqrt{(a - b - c)^{2}}-\sqrt{(a + b - c)^{2}}$的结果为（ ）
A.$2b$
B.$-2b$
C.$a + 2c$
D.$2c - 2a$

答案： D

17.若代数式$\sqrt{(2 - m)^{2}}-\sqrt{(m - 6)^{2}}$的值是4，则$m$的取值范围是________.

答案： m≥6

18.化简：$\sqrt{a^{2}-6a + 9}+\sqrt{a^{2}-14a + 49}(3\leqslant a\leqslant7)$.

答案： 解:原式=$\sqrt{(a - 3)^{2}}+\sqrt{(a - 7)^{2}}=\vert a - 3\vert+\vert a - 7\vert$,
∵3≤ a ≤ 7,
∴ a - 3≥ 0,a - 7≤ 0,
∴原式=a - 3+7 - a = 4.

19.若实数$a$，$b$满足$b＜\sqrt{2a - 1}+\sqrt{1 - 2a}+3$.试化简：$\frac{\sqrt{4a^{2}-4a + 1}+\sqrt{b^{2}-6b + 9}}{b - 3}$.

答案： 解:由题意,得$\begin{cases}2a - 1\geqslant0\\1 - 2a\geqslant0\end{cases}$,解得$a=\frac{1}{2}$,
∴ b ＜ 3.
∴ b - 3 ＜ 0.
∴原式=$\sqrt{(2a - 1)^{2}}+\frac{\sqrt{(b - 3)^{2}}}{b - 3}=\vert 2a - 1\vert+\frac{\vert b - 3\vert}{b - 3}=0+\frac{-(b - 3)}{b - 3}=-1$.