《2025年课堂点睛八年级数学下册人教版安徽专版》

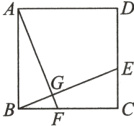
教材母题:如图，ABCD是一个正方形花园，E,F是它的两个门，且DE=CF.要修建两条路BE和AF，这两条路等长吗？它们有什么位置关系？为什么？
　　　　　　　　　　　　

答案： 解:$BE = AF$且$BE⊥AF$,理由:
∵四边形ABCD是正方形,
∴$AB = AD=CD$,$∠BAD = ∠D = 90^{\circ}$.又
∵$DE = CF$,
∴$AE = DF$,
∴$\triangle ABE\cong\triangle DAF$(SAS),
∴$BE = AF$,$∠ABE = ∠DAF$.设$BE,AF$交于点G,
∵$∠DAF + ∠BAF=90^{\circ}$,
∴$∠ABE + ∠BAF = 90^{\circ}$.
∴$∠AGB = 90^{\circ}$.
∴$BE⊥AF$.

1.如图，点E,F分别是正方形ABCD的边CD,BC上的点，且CE=BF，AF,BE相交于点G，则下列结论不正确的是 （ ）
A.AF=BE
B.AF⊥BE
C.AG=GE
D.$S_{△ABG}$=$S_{四边形CEGF}$
　　　　　　　　　　　　

答案： C

2.(贵阳市模拟)如图，在正方形ABCD中，E为AD上一点，连接BE，BE的垂直平分线交AB于点M，交CD于点N，垂足为O，点F在DC上，且MF//AD.求证:AE=FN.

答案： 证明:
∵正方形ABCD,
∴$AB = AD,AB// CD,∠A = 90^{\circ}=∠D$.又
∵$MF// AD$,
∴四边形AMFD是平行四边形,$∠D = ∠MFC = 90^{\circ}$.又
∵$∠A = 90^{\circ}$,
∴$\square AMFD$是矩形.
∴$MF = AD = AB$.
∵BE的垂直平分线交AB于点M,交CD于点N,垂足为O,
∴$∠FMN + ∠BMO = ∠BMO + ∠MBO = 90^{\circ}$,
∴$∠FMN = ∠MBO$.又
∵$AB=FM,∠A = ∠MFN$,
∴$\triangle ABE\cong\triangle FMN$.
∴$AE = FN$.

3.(哈尔滨市中考)已知四边形ABCD是正方形，点E在边DA的延长线上，连接CE交AB于点G，过点B作BM⊥CE，垂足为M，BM的延长线交AD于点F，交CD的延长线于点H.
(1)如图1，求证:CE=BH；
(2)如图2，若AE=AB，连接CF，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形(△AEG除外)，使写出的每个三角形都与△AEG全等.
　　　　　　 　　　

答案：
(1)证明:
∵四边形ABCD是正方形,
∴$BC = CD = AD = AB,∠BCD = ∠ADC = 90^{\circ}$.
∵BM⊥CE,
∴$∠HMC=∠ADC = 90^{\circ}$.
∴$∠H + ∠ECD=∠E + ∠ECD=90^{\circ}$.
∴$∠H=∠E$.在$\triangle EDC$和$\triangle HCB$中,$\begin{cases} \angle E=\angle H \\ \angle EDC=\angle HCB \\ CD=BC \end{cases}$,
∴$\triangle EDC\cong\triangle HCB$(AAS).
∴$CE = BH$.
(2)解:$\triangle BCG,\triangle DCF,\triangle DHF,\triangle ABF$.