第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
10.(广西自治区中考)如图,在▱ABCD中,∠B = 60°,AB = 6cm,BC = 12cm,点P从点A出发.以1cm/s的速度沿A→D运动,同时点Q从点C出发,以3cm/s的速度沿C→B→C→…往复运动,当点P到达端点D时,点Q随之停止运动,在此运动过程中,线段PQ = CD出现的次数是( )
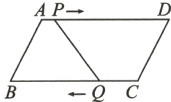
A.3
B.4
C.5
D.6
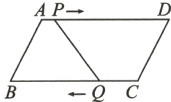
A.3
B.4
C.5
D.6
答案:
B
11.(河南省中考)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN = AB = 1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为______.
答案:
2或1 + √2
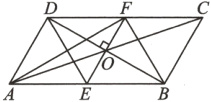
12.如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA = OC,OB = OD,过点O作EF⊥BD,分别交AB,DC于点E,F,连接DE,BF.
(1)求证:四边形DEBF是菱形;
(2)设AD//EF,AD + AB = 12,BD = 4$\sqrt{3}$,求AF的长.
(1)求证:四边形DEBF是菱形;
(2)设AD//EF,AD + AB = 12,BD = 4$\sqrt{3}$,求AF的长.

答案:
(1)证明:
∵OA = OC , OB = OD ,
∴四边形ABCD是平行四边形 , AB//CD .
∴∠ABD=∠CDB . 在△BOE和△DOF中,{∠EBO=∠FDO,OB = OD,∠BOE=∠DOF},
∴△BOE≌△DOF(ASA).
∴OE = OF,
∴四边形DEBF是平行四边形.
∵EF⊥BD,
∴四边形DEBF是菱形.
(2)解:过点F作FG⊥AB于点G.
∵AD//EF,EF⊥BD,
∴在Rt△ABD中,AD²+BD²=AB².
∵AD + AB = 12,设AD = x,则AB = 12 - x,所以x²+BD²=(12 - x)².解得AD = 4,
∴AB = 8.因为四边形DEBF是菱形,
∴∠EBF = 2∠ABD = 60°,BE = BF,所以△BEF是等边三角形.易知∠GFB = 30°,设BG = y,则BF = 2y,FG = √3y.在Rt△BGF中,由勾股定理,得y²+(√3y)²=(2y)²,解得BG = 2.
∴AG = AB - BG = 8 - 2 = 6.在Rt△AGF中,根据勾股定理,得AF=√(AG²+FG²)=√(6²+(2√3)²) = 4√3
(1)证明:
∵OA = OC , OB = OD ,
∴四边形ABCD是平行四边形 , AB//CD .
∴∠ABD=∠CDB . 在△BOE和△DOF中,{∠EBO=∠FDO,OB = OD,∠BOE=∠DOF},
∴△BOE≌△DOF(ASA).
∴OE = OF,
∴四边形DEBF是平行四边形.
∵EF⊥BD,
∴四边形DEBF是菱形.
(2)解:过点F作FG⊥AB于点G.
∵AD//EF,EF⊥BD,
∴在Rt△ABD中,AD²+BD²=AB².
∵AD + AB = 12,设AD = x,则AB = 12 - x,所以x²+BD²=(12 - x)².解得AD = 4,
∴AB = 8.因为四边形DEBF是菱形,
∴∠EBF = 2∠ABD = 60°,BE = BF,所以△BEF是等边三角形.易知∠GFB = 30°,设BG = y,则BF = 2y,FG = √3y.在Rt△BGF中,由勾股定理,得y²+(√3y)²=(2y)²,解得BG = 2.
∴AG = AB - BG = 8 - 2 = 6.在Rt△AGF中,根据勾股定理,得AF=√(AG²+FG²)=√(6²+(2√3)²) = 4√3
查看更多完整答案,请扫码查看


