《2025年课堂点睛八年级数学下册人教版安徽专版》

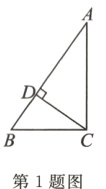
1. 如图，在△ABC中，∠ACB = 90°，CD⊥AB于D. 若AC = 2√3，BC = √6，则CD = （ ）
A. √2 B. 2 C. √3 D. 3
　

答案： B

2. 如图，在3×3的网格中，每个小正方形的边长均为1，点A，B，C都在格点上. 若BD是△ABC的高，则BD的长为__________.
　

答案： $\frac{7\sqrt{13}}{13}$

3. 点A，B，C在格点图中的位置如图所示. 若格点小正方形的边长均为1，则点C到线段AB所在直线的距离为__________.
　

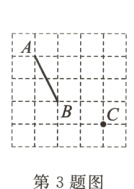
答案： $\frac{3\sqrt{5}}{5}$

4. 已知Rt△ABC中，∠C = 90°，若a + b = 12，c = 10，则Rt△ABC的面积是 （ ）
A. 48
B. 24
C. 16
D. 11

答案： D

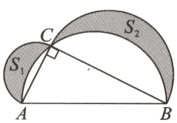
5. 如图，阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形，面积分别记作S₁和S₂. 若S₁ + S₂ = 30，AB = 13，则△ABC的周长是 （ ）
A. 26
B. 43
C. 30
D. 28
　

答案： C

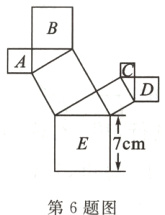
6. 在如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积的和是______cm².
　

答案： 49

7. (扬州市中考)我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成. 如图，直角三角形的直角边长为a，b，斜边长为c，若b - a = 4，c = 20，则每个直角三角形的面积为______.
　

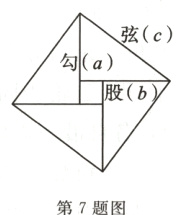
答案： 96

8. 如图，已知∠ADC = 90°，AD = 8m，CD = 6m，BC = 24m，AB = 26m，则四边形ABCD的面积为__________.
　

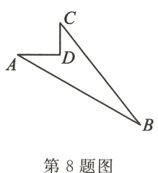
答案： $96m^{2}$

9. 如图，∠B = ∠D = 90°，∠A = 60°，AB = 2，CD = 1，则四边形ABCD的面积为__________.
　

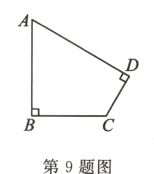
答案： $\frac{3\sqrt{3}}{2}$