《2025年课堂点睛八年级数学下册人教版安徽专版》

1.四边形ABCD中,对角线AC,BD相交于点O.给出下列四个条件:①AD//BC;②AD = BC;③OA = OC;④OB = OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有（ ）
A.3种
B.4种
C.5种
D.6种

答案： B

2.(天津市中考)如图,▱ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是（ ）

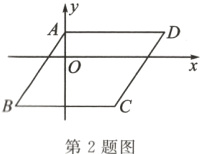
A.(-4,1)
B.(4,-2)
C.(4,1)
D.(2,1)

答案： C

3.(贵阳市中考)如图,在▱ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,若AB = 3,AD = 4.则EF的长是（ ）

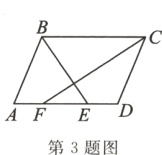
A.1
B.2
C.2.5
D.3

答案： B

4.(岳阳市中考)如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.
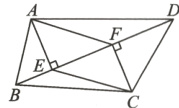
(1)请你只添加一个条件(不另加辅助线),使得四边形AECF为平行四边形,你添加的条件是____________________;
(2)在(1)中添加的条件的前提下,求证:四边形AECF为平行四边形.

答案：
(1)AE = CF(答案不唯一)
(2)证明:
∵AE⊥BD,CF⊥BD ,
∴∠AEF = ∠CFE=90°.
∴AE//CF.
∵AE = CF ,
∴四边形AECF为平行四边形.

5.(丽水市中考)如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB = 6,BC = 8,则四边形BDEF的周长是（ ）

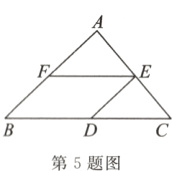
A.26
B.14
C.10
D.7

答案： B

6.(郴州市中考)如图,在Rt△ABC中,∠ACB = 90°,AC = 6,BC = 8,点M是AB的中点,则CM = ______.

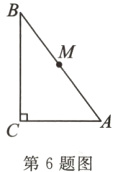
答案： 5

7.(广州市中考)给出下列命题:①对角线互相平分的四边形是平行四边形;②对角线互相垂直的四边形是菱形;③对角线相等的平行四边形是菱形;④有一个角是直角的平行四边形是矩形.其中,属于真命题的是（ ）
A.①②
B.①④
C.②④
D.③④

答案： B

8.如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为______cm.

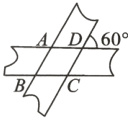
答案： 8√3

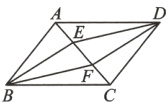
9.(呼和浩特市中考)如图,四边形ABCD是平行四边形,BE//DF且分别交对角线AC于点E,F.
(1)求证:△ABE≌△CDF;
(2)连接BF,DE,当四边形ABCD分别是矩形和菱形时,请直接写出四边形BEDF的形状.

答案：
(1)证明:
∵四边形ABCD是平行四边形 ,
∴AB = CD , AB//CD .
∴∠BAE=∠DCF .
∵BE//DF ,
∴∠BEC=∠DFA .
∵∠BEC + ∠AEB=180° , ∠DFA + ∠CFD=180° ,
∴∠AEB=∠CFD . 在△ABE和△CDF中,{∠AEB=∠CFD,∠BAE=∠DCF,AB = CD},
∴△ABE≌△CDF .
(2)解:当四边形ABCD是矩形时 ,四边形BEDF是平行四边形;当四边形ABCD是菱形时 ,四边形BEDF是菱形.