《2025年课堂点睛八年级数学下册人教版安徽专版》

1. 若$x$为任意实数，下列各式一定是二次根式的是（ ）
A. $\sqrt{x^2 - 1}$
B. $\sqrt{x^2 + 1}$
C. $\sqrt{3x}$
D. $\sqrt{x + 1}$

答案： B

2. (常德市中考)要使代数式$\frac{x}{\sqrt{x - 4}}$有意义，则$x$的取值范围为________.

答案： $x＞4$

3. (遂宁市中考)实数$a$，$b$在数轴上的位置如图所示，化简：$\vert a + 1\vert - \sqrt{(b - 1)^2} + \sqrt{(a - b)^2}=$_____.
　

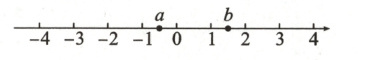
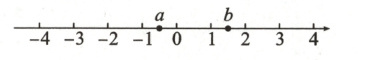
答案： 2

4. 若$m = \sqrt{n - 2} + \sqrt{2 - n} + 5$，则$m^n =$_____.

答案： 25

5. 若$\sqrt{x^2}=(\sqrt{2025})^2$，则$x =$________.

答案： $\pm2025$

6. 下列各式是最简二次根式的是（ ）
A. $\sqrt{13}$
B. $\sqrt{12}$
C. $\sqrt{a^3}$
D. $\sqrt{\frac{5}{3}}$

答案： A

7. (重庆市中考)下列计算中，正确的是（ ）
A. $5\sqrt{7}-2\sqrt{7}=21$
B. $2+\sqrt{2}=2\sqrt{2}$
C. $\sqrt{3}\times\sqrt{6}=3\sqrt{2}$
D. $\sqrt{15}\div\sqrt{5}=3$

答案： C

8. (宜昌市中考改编)对于无理数$\sqrt{3}$，添加关联的数或者运算符号组成新的式子，其运算结果能成为有理数的是（ ）
A. $2\sqrt{3}-3\sqrt{2}$
B. $\sqrt{3}+\sqrt{3}$
C. $(\sqrt{3})^3$
D. $0\times\sqrt{3}$

答案： D

9. (结论开放)从$-\sqrt{2}$，$\sqrt{3}$，$\sqrt{6}$中任意选择两个数，分别填在算式$(□ + ○)^2\div\sqrt{2}$里面的“$□$”与“$○$”中，计算该算式的结果是______________________.(只需写出一种结果)

答案： $\frac{5\sqrt{2}}{2}-2\sqrt{3}$（答案不唯一）

10. 计算：
(1) $(\sqrt{48}-3\sqrt{\frac{1}{3}})\div\sqrt{3}$；
(2) $(\sqrt{\frac{1}{2}}+\sqrt{3})-(\sqrt{2}-\sqrt{12})+\frac{\sqrt{2}}{2}$；
(3) $(\sqrt{5}+3)(\sqrt{5}-3)-(\sqrt{3}-1)^2+8$.

答案： （1）解：原式$=(4\sqrt{3}-\sqrt{3})\div\sqrt{3}=3$. （2）解：原式$=\frac{\sqrt{2}}{2}+\sqrt{3}-\sqrt{2}+2\sqrt{3}+\frac{\sqrt{2}}{2}=3\sqrt{3}-\sqrt{2}+\sqrt{2}=3\sqrt{3}$. （3）解：原式$=(\sqrt{5})^{2}-3^{2}-(3 - 2\sqrt{3}+1)+8=5 - 9 - 4 + 2\sqrt{3}+8=2\sqrt{3}-8 + 8=2\sqrt{3}$.