《2025年课堂点睛八年级数学下册人教版安徽专版》

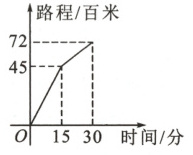
10.小亮早晨从家骑车去学校，先走下坡路，然后走上坡路，去时行程情况如图所示，若返回时，他的下坡和上坡速度仍保持不变，那么小亮从学校按原路返回到家所用的时间是______分钟.

答案： 34

11.根据记录，从地面向上11km以内（含11km），每升高1km，气温降低6℃；又知在距离地面11km以上高空，气温几乎不变.若地面气温为m(℃)，设距地面的高度为x(km)处的气温为y(℃).
(1)距地面的高度在11km以内（含11km）的y与x之间的函数解析式为____________________；
(2)当x=7，y= - 26，求地面的温度.

答案：
(1)$y = m - 6x(0\leqslant x\leqslant11)$
(2)解:把$x = 7,y = -26$代入解析式$y = m - 6x$,得$-26 = m - 6\times7$,解得$m = 16$.答:地面的温度为$16^{\circ}C$.

12.（核心素养·运算能力）某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨2.5元收费，如果超过20吨，未超过的部分按每吨2.5元收费，超过的部分按每吨3.3元收费.设某户每月用水量为x吨，应缴水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨时，y与x间的函数关系式；
(2)若该城市某户4月份水费平均为每吨2.8元，求该户4月份用水多少吨？

答案：
(1)解:当$x\leqslant20$时,$y = 2.5x$;当$x ＞ 20$时,$y = 3.3(x - 20)+2.5\times20 = 3.3x - 16$.
(2)
∵该户4月份水费平均每吨2.8元,
∴该户4月份用水超过了20吨.设该户4月份用水$a$吨,得$2.8a = 3.3a - 16$,解得$a = 32$.答:该户4月份用水32吨.

13.已知点P(x，y)是第一象限内的点，且x + y=8，点A的坐标为(10，0).设三角形OAP的面积为S.
(1)求S与x之间的函数表达式，并写出自变量的取值范围；
(2)画出S关于x的函数图象.

答案：
解:由$x + y = 8$得，$y = 8 - x$,三角形OAP的面积$S=\frac{1}{2}\cdot OA\cdot|y|=\frac{1}{2}\times10\times|8 - x|=5(8 - x)=40 - 5x$.由$P(x,y)$在第一象限,得$\begin{cases}x＞0\\8 - x＞0\end{cases}$,解得$0 ＜ x ＜ 8$,故$S = 40 - 5x(0 ＜ x ＜ 8)$.
(2)画函数图象如图.